Advertisements
Advertisements
प्रश्न
A proton goes undeflected in a crossed electric and magnetic field (the fields are perpendicular to each other) at a speed of 2.0 × 105 m s−1. The velocity is perpendicular to both the fields. When the electric field is switched off, the proton moves along a circle of radius 4.0 cm. Find the magnitudes of the electric and magnetic fields. Take the mass of the proton = 1.6 × 10−27 kg
उत्तर
Given:
Mass of the proton, m = 1.6 × 10−27 kg
Speed of the proton inside the crossed electric and magnetic field, v = 2.0 × 105 ms−1
As per the question, the proton is not deflected under the combined action of the electric and magnetic fields. Thus, the forces applied by both the fields are equal and opposite.
That is, qE = qvB
⇒ E = vB ...(1)
But when the electric field is switched off, the proton moves in a circle due to the force of the magnetic field.
Radius of the circle, r = 4.0 cm = 4 × 10−2 m
We know: r = `(mv)/(qB)`
⇒ `(1.6xx10^-27xx2xx10^5)/(1.6xx100^194xx10^-3`)
= 0.5 × 10−1 = 0.05 T
Putting the value of B in equation (1), we get:
E = 2 × 105 × 0.05
= 1 × 104 N/c
APPEARS IN
संबंधित प्रश्न
State Biot – Savart law.
Express Biot – Savart law in the vector form.
State Biot-Savart law.
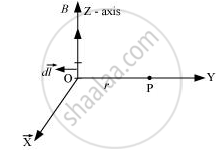
A current I flows in a conductor placed perpendicular to the plane of the paper. Indicate the direction of the magnetic field due to a small element d `vecl` at point P situated at distance `vecr` from the element as shown in the figure.
An alpha particle is projected vertically upward with a speed of 3.0 × 104 km s−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the α-particle.
The magnetic field at the origin due to a current element \[i d \vec{l}\] placed at a position \[\vec{r}\] is
(a)\[\frac{\mu_0 i}{4\pi}\frac{d \vec{l} \times \vec{r}}{r^3}\]
(b) \[- \frac{\mu_0 i}{4\pi}\frac{\vec{r} \times d \vec{l}}{r^3}\]
(c) \[\frac{\mu_0 i}{4\pi}\frac{\vec{r} \times d \vec{l}}{r^3}\]
(d) \[- \frac{\mu_0 i}{4\pi}\frac{d \vec{l} \times \vec{r}}{r^3}\]
A long, vertical wire carrying a current of 10 A in the upward direction is placed in a region where a horizontal magnetic field of magnitude 2.0 × 10−3 T exists from south to north. Find the point where the resultant magnetic field is zero.
An electric current I flows through a circular loop as shown in Figure 2(b) below. Write an expression and direction for the magnetic field at the centre of the loop at point P.
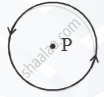
State and explain the law used to determine magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current carrying loop of radius r at its centre.
A long wire with a small current element of length 1 cm is placed at the origin and carries a current of 10 A along the X-axis. Find out the magnitude and direction of the magnetic field due to the element on the Y-axis at a distance 0.5 m from it.
Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
A straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the centre of the arc.

State Biot Savart law.
Derive the expression for the magnetic field due to a current-carrying coil of radius r at a distance x from the center along the X-axis.
A straight wire carrying a current of 5 A is bent into a semicircular arc radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the center of the arc

Two concentric circular loops of radius 1 cm and 20 cm are placed coaxially.
(i) Find mutual inductance of the arrangement.
(ii) If the current passed through the outer loop is changed at a rate of 5 A/ms, find the emf induced in the inner loop. Assume the magnetic field on the inner loop to be uniform.
Biot-Savart law indicates that the moving electrons (velocity v) produce a magnetic field B such that ______.
- both are long range and inversely proportional to the square of distance from the source to the point of interest.
-
both are linear in source.
-
both are produced by scalar sources.
-
both follow principle of superposition.
A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude of B at the origin.
