Advertisements
Advertisements
प्रश्न
A rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the x-axis.
Advertisements
उत्तर
Let OX, OY be coordinates. The line PQ = 12 cm runs on these axes.
∆ POQ में, PQ2 = OP2 + OQ2
122 = a2 + b2
or a2 + b2 = 144 ......(i)
Where OA = a, OB = b are the intercepts on the axes.
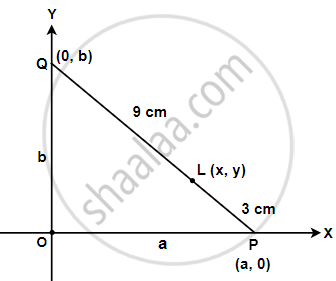
The point L(x, y) divides PQ in the ratio 3 : 9 = 1 : 3. Whereas the coordinates of P and Q are (a, 0) and (0, b) respectively.
∴ The coordinates of I3 will be as follows:
`x = (3a + 1 xx 0)/(3 + 1) = (3a)/4`
∴ a = `(4x)/3`
y = `(3 xx 0 + 1 xx b)/(3 + 1) = b/4`
∴ b = 4y
Putting their values in equation (i),
`(4/3x)^2 + (4y)^2 = 144`
or `(16x^2)/9 + (16y^2)/1 = 144`
or `x^2/9 + y^2 /1 = 9`
Hence, the locus of L is an ellipse. Whose equation is `x^2/81 + y^2/9 = 1`.
APPEARS IN
संबंधित प्रश्न
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
`x^2/25 + y^2/100 = 1`
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
`x^2/49 + y^2/36 = 1`
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
`x^2/100 + y^2/400 = 1`
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
36x2 + 4y2 = 144
An arch is in the form of a semi-ellipse. It is 8 m wide and 2 m high at the centre. Find the height of the arch at a point 1.5 m from one end.
Find the vertex, focus, axis, directrix and latus-rectum of the following parabola:
y2 = 8x
Find the vertex, focus, axis, directrix and latus-rectum of the following parabola
y2 = 8x + 8y
Find the vertex, focus, axis, directrix and latus-rectum of the following parabola
y2 = 8x + 8y
Find the vertex, focus, axis, directrix and latus-rectum of the following parabola
4 (y − 1)2 = − 7 (x − 3)
Find the length of the line segment joining the vertex of the parabola y2 = 4ax and a point on the parabola where the line-segment makes an angle θ to the x-axis.
Write the axis of symmetry of the parabola y2 = x.
Write the coordinates of the vertex of the parabola whose focus is at (−2, 1) and directrix is the line x + y − 3 = 0.
In the parabola y2 = 4ax, the length of the chord passing through the vertex and inclined to the axis at π/4 is
The vertex of the parabola (y − 2)2 = 16 (x − 1) is
Find the centre, the lengths of the axes, eccentricity, foci of the following ellipse:
x2 + 4y2 − 4x + 24y + 31 = 0
Find the centre, the lengths of the axes, eccentricity, foci of the following ellipse:
3x2 + 4y2 − 12x − 8y + 4 = 0
Find the centre, the lengths of the axes, eccentricity, foci of the following ellipse:
4x2 + 16y2 − 24x − 32y − 12 = 0
Find the centre, the lengths of the axes, eccentricity, foci of the following ellipse:
x2 + 4y2 − 2x = 0
Find the equation of an ellipse whose foci are at (± 3, 0) and which passes through (4, 1).
Find the equation of the set of all points whose distances from (0, 4) are\[\frac{2}{3}\] of their distances from the line y = 9.
Write the eccentricity of the ellipse 9x2 + 5y2 − 18x − 2y − 16 = 0.
If S and S' are two foci of the ellipse \[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\] and B is an end of the minor axis such that ∆BSS' is equilateral, then write the eccentricity of the ellipse.
If the minor axis of an ellipse subtends an equilateral triangle with vertex at one end of major axis, then write the eccentricity of the ellipse.
If a latus rectum of an ellipse subtends a right angle at the centre of the ellipse, then write the eccentricity of the ellipse.
The equation of the circle having centre (1, –2) and passing through the point of intersection of the lines 3x + y = 14 and 2x + 5y = 18 is ______.
The equation of the ellipse whose centre is at the origin and the x-axis, the major axis, which passes through the points (–3, 1) and (2, –2) is ______.
If the lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to a circle, then find the radius of the circle.
The shortest distance from the point (2, –7) to the circle x2 + y2 – 14x – 10y – 151 = 0 is equal to 5.
