Advertisements
Advertisements
प्रश्न
AB and CD are the smallest and largest sides of a quadrilateral ABCD. Out of ∠B and ∠D decide which is greater.
उत्तर
Given: In quadrilateral ABCD, AB is the smallest and CD is the largest side
To find: ∠B > ∠D or ∠D > ∠B.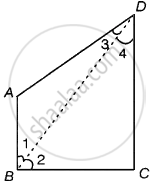
Construction: Join BD.
Now, in ΔABD, AD > AB ...[Since, AB is the smallest side in ABCD]
⇒ ∠1 > ∠3 [Angle opposite to larger side is greater] ...(i)
In ΔBCD, CD > BC ...[Since, CD is the largest side in ABCD]
⇒ ∠2 > ∠4 [Angle opposite to larger side is greater] ...(ii)
On adding equations (i) and (ii), we get
∠1 + ∠2 > ∠3 + ∠4
Hence, ∠B > ∠D
APPEARS IN
संबंधित प्रश्न
Is the following statement true and false :
A triangle can have at most one obtuse angles.
In a Δ ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q, Prove that ∠BPC + ∠BQC = 180°.
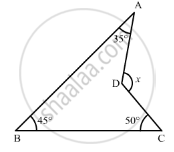
In the given figure, compute the value of x.
One angle of a triangle is 60°. The other two angles are in the ratio of 5: 7. Find the two angles.
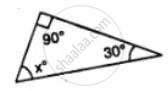
Calculate the unknown marked angles of the following figure :
Can a triangle together have the following angles?
33°, 74° and 73°
The exterior angle of a triangle is equal to the sum of two
In ΔABC, name the 
a) Three sides: _________, __________, __________
b) Three Angles: _________, __________, __________
c) Three Vertices: _________, __________, __________
S is any point on side QR of a ∆PQR. Show that: PQ + QR + RP > 2PS.
P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
