Advertisements
Advertisements
प्रश्न
एक A.P. में, a3 = 15 और S10 = 125 दिया है। d और a10 ज्ञात कीजिए।
उत्तर
दिया गया है कि, a3 = 15, S10 = 125
चूँकि an = a + (n − 1)d,
a3 = a + (3 − 1)d
15 = a + 2d ...(i)
Sn =
S10 =
125 = 5(2a + 9d)
25 = 2a + 9d ...(ii)
समीकरण (i) को (ii) से गुणा करने पर, हमें मिलता है
30 = 2a + 4d ...(iii)
समीकरण (iii) को (ii) से घटाने पर, हमें मिलता है
−5 = 5d
d = −1
समीकरण (i) से,
15 = a + 2(−1)
15 = a − 2
a = 17
a10 = a + (10 − 1)d
a10 = 17 + (9) (−1)
a10 = 17 − 9
a10 = 8
APPEARS IN
संबंधित प्रश्न
0 और 50 के बीच की विषम संख्याओं का योग ज्ञात कीजिए।
केंद्र A से प्रारंभ करते हुए, बारी-बारी से केंद्रों A और B को लेते हुए, त्रिज्याओं 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm,……. वाले उतरोत्तर अर्धवृत्तों को खींचकर एक सर्पिल (Spiral) बनाया गया है, जैसाकि आकृति में दर्शाया गया है। तेरह क्रमागत अर्धवृत्तों से बने इस सर्पिल की कुल लंबाई क्या है? (π =
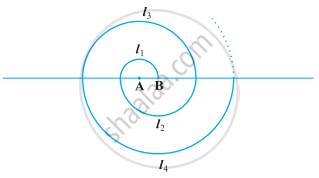
[संकेत: क्रमशः केंद्रों A, B, A, B,... वाले अर्धवृत्तों की लंबाइयाँ l1, l2, l3, l4 हैं।]
प्रथम 100 प्राकृत संख्याओं के योग को ज्ञात करने से संबद्ध प्रसिद्ध गणितज्ञ ______ है।
AP:
योग ज्ञात कीजिए :
1 + (–2) + (–5) + (–8) + ... + (–236)
योग ज्ञात कीजिए :
किसी AP में यदि Sn = 3n2 + 5n और ak = 164 है, तो k का मान ज्ञात कीजिए।
उस AP के प्रथम 17 पदों का योग ज्ञात कीजिए, जिसके चौथे और 9 वें पद क्रमशः –15 और –30 हैं।
ऐसी प्रथम सात संख्याओं का योग ज्ञात कीजिए, जो 2 का गुणज हैं और 9 का भी गुणज हैं।
[संकेत : 2 और 9 का LCM ज्ञात कीजिए।]
दर्शाइए कि उस AP का योग, जिसका प्रथम पद a, द्वितीय पद b और अंतिम पद c हो,
