Advertisements
Advertisements
प्रश्न
किसी AP में यदि Sn = 3n2 + 5n और ak = 164 है, तो k का मान ज्ञात कीजिए।
उत्तर
∵ किसी AP का n वाँ पद,
an = Sn – Sn – 1
= 3n2 + 5n – 3(n – 1)2 – 5(n – 1) ...[∵ Sn = 3n2 + 5n (दिया गया है)]
= 3n2 + 5n – 3n2 – 3 + 6n – 5n + 5
⇒ an = 6n + 2 ...(i)
या ak = 6k + 2 = 164 ...[∵ ak = 164 (दिया गया है)]
⇒ 6k = 164 – 2 = 162
∴ k = 27
APPEARS IN
संबंधित प्रश्न
निम्नलिखित समांतर श्रेढ़ी का योग ज्ञात कीजिए:
2, 7, 12, ......,10 पदों तक
8 के प्रथम 15 गुणजों का योग ज्ञात कीजिए।
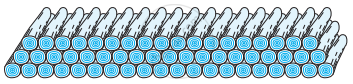
200 लट्ठों (logs) को ढेरी के रूप में इस प्रकार रखा जाता है : सबसे नीचे वाली पंक्ति में 20 लट्ठे, उससे अगली पंक्ति में 19 लट्ठे, उससे अगली पंक्ति में 18 लट्ठे, इत्यादि (देखिए आकृति)। ये 200 लठ्ठे कितनी पंक्तियों में रखे गए हैं तथा सबसे ऊपरी पंक्ति में कितने लट्ठे हैं?
उस AP के प्रथम 17 पदों का योग ज्ञात कीजिए, जिसके चौथे और 9 वें पद क्रमशः –15 और –30 हैं।
AP: 8, 10, 12,..., 126 के अंतिम 10 पदों का योग ज्ञात कीजिए।
ऐसी प्रथम सात संख्याओं का योग ज्ञात कीजिए, जो 2 का गुणज हैं और 9 का भी गुणज हैं।
[संकेत : 2 और 9 का LCM ज्ञात कीजिए।]
AP: −15, −13, −11,... का योग −55 बनाने के लिए इसके कितने पदों की आवश्यकता होगी? दो उत्तर प्राप्त होने का कारण स्पष्ट कीजिए।
ज्ञात कीजिए :
1 और 500 के बीच के उन पूर्णांकों का योग जो 2 के भी गुणज हैं और 5 के भी गुणज हैं।
किसी AP में 37 पद हैं। बीचो-बीच के तीन पदों का योग 225 है तथा अंतिम तीन पदों का योग 429 है। वह AP ज्ञात कीजिए।
दर्शाइए कि उस AP का योग, जिसका प्रथम पद a, द्वितीय पद b और अंतिम पद c हो, `((a + c)(b + c - 2a))/(2(b - a))` के बराबर है।
