Advertisements
Advertisements
प्रश्न
Find the area, in square metres, of the trapezium whose bases and altitude is as under:
bases = 28 cm and 3 dm, altitude = 25 cm
उत्तर
Given:
Bases:
\[28 cm =\frac{28}{100}m = 0.28 m\]
And, 3 dm \[=\frac{3}{10}m = 0.3 m\]
Altitude = 25 cm\[ =\frac{25}{100}m = 0.25 m\]
Area of trapezium \[=\frac{1}{2}\times(\text{ Sum of the bases })\times( \text{ Altitude })\]
\[ = \frac{1}{2} \times (0 . 28 + 0 . 3) m \times (0 . 25) m\]
\[ {= 0.0725 m}^2 \]
APPEARS IN
संबंधित प्रश्न
Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.

Find the height of a trapezium, the sum of the lengths of whose bases (parallel sides) is 60 cm and whose area is 600 cm2.
Find the sum of the lengths of the bases of a trapezium whose area is 4.2 m2 and whose height is 280 cm.
Find the area of a trapezium whose parallel sides of lengths 10 cm and 15 cm are at a distance of 6 cm from each other. Calculate this area as the difference of the area of a rectangle and the sum of the areas of two triangles.
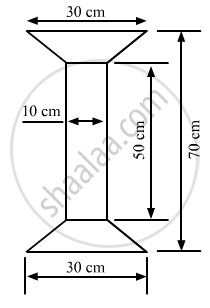
Find the area of Fig. as the sum of the areas of two trapezium and a rectangle.
Find the area of the pentagon shown in fig. 20.48, if AD = 10 cm, AG = 8 cm, AH = 6 cm, AF = 5 cm, BF = 5 cm, CG = 7 cm and EH = 3 cm.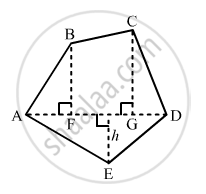
The following figure shows the cross-section ABCD of a swimming pool which is a trapezium in shape.
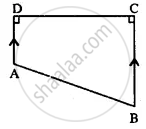
If the width DC, of the swimming pool, is 6.4 m, depth (AD) at the shallow end is 80 cm and depth (BC) at the deepest end is 2.4 m, find its area of the cross-section.
When the non-parallel sides of a trapezium are equal then it is known as
The area of a trapezium become 4 times if its height gets doubled.
The areas of two circles are in the ratio 49 : 64. Find the ratio of their circumferences.
