Advertisements
Advertisements
प्रश्न
Find the dimensions of the rectangle of perimeter 36 cm which will sweep out a volume as large as possible, when revolved about one of its sides. Also find the maximum volume.
उत्तर
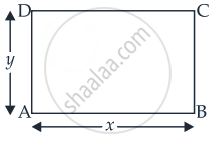
Let x and y be the length and breadth of a given rectangle ABCD as per question, the rectangle be revolved about side AD which will make a cylinder with radius x and height y.
∴ Volume of the cylinder V = `(pi"r"^2)/"h"`
⇒ V = `pix^2y` .....(i)
Now perimeter of rectangle P = 2(x + y)
⇒ 36 = 2(x + y)
⇒ x + y = 18
⇒ y = 18 – x ....(iii)
Putting the value of y in eq. (i) we get
V = `pix^2(18 - x)`
⇒ V = `pi(18x^2 - x^3)`
Differentiating both sides w.r.t. x, we get
`"dV"/"dx" = pi(36x - 3x^2)` ....(iii)
For local maxima and local minima `"dV"/"dx"` = 0
∴ `pi(36x - 3x^2)` = 0
⇒ 36x – 3x2 = 0
⇒ 3x(12 – x) = 0
⇒ x 0
∴ 12 – x = 0
⇒ x = 12
From equation (ii)
y = 18 – 12 = 6
Differentiating equation (iii) w.r.t. x,
We get `("d"^2"V")/("dx"^2) = pi(36 - 6x)`
At x = 12 `("d"^2"V")/("dx"^2)`
= `pi(36 - 6 xx 12)`
= `pi(36 - 72)`
= `- 36pi < 0` maxima
Now volume of the cylinder so formed = `pix^2y`
= `pi xx (12)^2 xx 6`
= `pi xx 144 xx 6`
= 864π cm3
Hence, the required dimensions are 12 cm and 6 cm and the maximum volume is 864π cm3
APPEARS IN
संबंधित प्रश्न
An open box is to be made out of a piece of a square card board of sides 18 cms by cutting off equal squares from the comers and turning up the sides. Find the maximum volume of the box.
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`h(x) = sinx + cosx, 0 < x < pi/2`
Find the absolute maximum value and the absolute minimum value of the following function in the given interval:
`f(x) =x^3, x in [-2,2]`
Find the maximum profit that a company can make, if the profit function is given by p(x) = 41 − 72x − 18x2.
Find the maximum value of 2x3 − 24x + 107 in the interval [1, 3]. Find the maximum value of the same function in [−3, −1].
Find the maximum and minimum values of x + sin 2x on [0, 2π].
Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is `8/27` of the volume of the sphere.
Find the maximum and minimum of the following functions : f(x) = x3 – 9x2 + 24x
A metal wire of 36cm long is bent to form a rectangle. Find it's dimensions when it's area is maximum.
If f(x) = 3x3 - 9x2 - 27x + 15, then the maximum value of f(x) is _______.
If R is the circum radius of Δ ABC, then A(Δ ABC) = ______.
The function y = 1 + sin x is maximum, when x = ______
The sum of two non-zero numbers is 6. The minimum value of the sum of their reciprocals is ______.
The sum of the surface areas of a rectangular parallelopiped with sides x, 2x and `x/3` and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of the sphere. Also find the minimum value of the sum of their volumes.
If y = x3 + x2 + x + 1, then y ____________.
Find the height of the cylinder of maximum volume that can be inscribed in a sphere of radius a.
The distance of that point on y = x4 + 3x2 + 2x which is nearest to the line y = 2x - 1 is ____________.
The range of a ∈ R for which the function f(x) = `(4a - 3)(x + log_e5) + 2(a - 7)cot(x/2)sin^2(x/2), x ≠ 2nπ, n∈N` has critical points, is ______.
A wire of length 36 m is cut into two pieces, one of the pieces is bent to form a square and the other is bent to form a circle. If the sum of the areas of the two figures is minimum, and the circumference of the circle is k (meter), then `(4/π + 1)`k is equal to ______.
If y = alog|x| + bx2 + x has its extremum values at x = –1 and x = 2, then ______.
The lateral edge of a regular rectangular pyramid is 'a' cm long. The lateral edge makes an angle a. with the plane of the base. The value of a for which the volume of the pyramid is greatest, is ______.
Let f(x) = |(x – 1)(x2 – 2x – 3)| + x – 3, x ∈ R. If m and M are respectively the number of points of local minimum and local maximum of f in the interval (0, 4), then m + M is equal to ______.
The maximum value of z = 6x + 8y subject to constraints 2x + y ≤ 30, x + 2y ≤ 24 and x ≥ 0, y ≥ 0 is ______.
Sum of two numbers is 5. If the sum of the cubes of these numbers is least, then find the sum of the squares of these numbers.
Complete the following activity to divide 84 into two parts such that the product of one part and square of the other is maximum.
Solution: Let one part be x. Then the other part is 84 - x
Letf (x) = x2 (84 - x) = 84x2 - x3
∴ f'(x) = `square`
and f''(x) = `square`
For extreme values, f'(x) = 0
∴ x = `square "or" square`
f(x) attains maximum at x = `square`
Hence, the two parts of 84 are 56 and 28.
Find the maximum and the minimum values of the function f(x) = x2ex.
Mrs. Roy designs a window in her son’s study room so that the room gets maximum sunlight. She designs the window in the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 m, find the dimensions of the window that will admit maximum sunlight into the room.