Advertisements
Advertisements
प्रश्न
Find the equation of the circle with centre at (a, b) touching the Y-axis
उत्तर
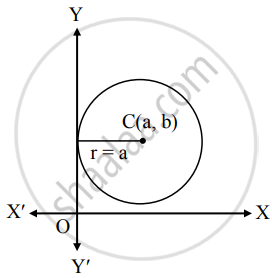
Since the circle is touching the Y-axis,
radius of the circle is X-co-ordinate of the centre.
∴ r = a
The equation of a circle with centre at (h, k) and radius r is given by
(x – h)2 + (y – k)2 = r2
Here, h = a, k = b
∴ The required equation of the circle is
(x – a)2 + (y – b)2 = a2
∴ x2 – 2ax + a2 + y2 – 2by + b2 = a2
∴ x2 + y2 – 2ax – 2by + b2 = 0
APPEARS IN
संबंधित प्रश्न
Find the equation of the circle with centre at (−3, −2) and radius 6.
Find the equation of the circle with centre at (2, −3) and radius 5.
Find the equation of the circle with centre at (−3, −3) passing through the point (−3, −6)
Find the centre and radius of the circle:
(x − 5)2 + (y − 3)2 = 20
Find the centre and radius of the circle:
`(x - 1/2)^2 + (y + 1/3)^2 = 1/36`
Find the equation of the circle with centre on the X-axis and passing through the origin having radius 4.
Find the equation of a circle with radius 4 units and touching both the co-ordinate axes having centre in third quadrant.
Find the equation of a circle passing through the points (1,−4), (5,2) and having its centre on the line x − 2y + 9 = 0
Find the centre and radius of the following:
x2 + y2 − 2x + 4y − 4 = 0
Find the centre and radius of the following:
4x2 + 4y2 − 24x − 8y − 24 = 0
Find the equation of the circle passing through the points (5, 7), (6, 6) and (2, −2)
Show that the points (3, −2), (1, 0), (−1, −2) and (1, −4) are concyclic
Choose the correct alternative:
If the lines 2x − 3y = 5 and 3x − 4y = 7 are the diameters of a circle of area 154 sq. units, then find the equation of the circle
Choose the correct alternative:
Area of the circle centre at (1, 2) and passing through (4, 6) is
Choose the correct alternative:
The equation of a circle with origin as centre and passing through the vertices of an equilateral triangle whose median is of length 3a is
Answer the following :
Find the centre and radius of the circle x2 + y2 − x +2y − 3 = 0
Answer the following :
Find the equation of circle passing through the point of intersection of the lines x + 3y = 0 and 2x − 7y = 0 whose centre is the point of intersection of lines x + y + 1 = 0 and x − 2y + 4 = 0
Answer the following :
Find the equation of circle which passes through the origin and cuts of chords of length 4 and 6 on the positive side of x-axis and y-axis respectively
Answer the following :
Show that the points (9, 1), (7, 9), (−2, 12) and (6, 10) are concyclic
Answer the following :
Find the equation of the circle concentric with x2 + y2 – 4x + 6y = 1 and having radius 4 units
Answer the following :
Show that the circles touch each other externally. Find their point of contact and the equation of their common tangent:
x2 + y2 – 4x – 10y + 19 = 0,
x2 + y2 + 2x + 8y – 23 = 0.
Answer the following :
Show that the circles touch each other internally. Find their point of contact and the equation of their common tangent:
x2 + y2 + 4x – 12y + 4 = 0,
x2 + y2 – 2x – 4y + 4 = 0
If 2x - 4y = 9 and 6x - 12y + 7 = 0 are the tangents of same circle, then its radius will be ______
The centre of the circle x = 3 + 5 cos θ, y = - 4 + 5 sin θ, is ______
The radius of a circle is increasing uniformly at the rate of 2.5cm/sec. The rate of increase in the area when the radius is 12cm, will be ______
If x2 + (2h - 1)xy + y2 - 24x - 8y + k = 0 is the equation of the circle and 12 is the radius of the circle, then ______.
The equation of the circle with centre (4, 5) which passes through (7, 3) is ______.
The equation of a circle with centre at (1, 0) and circumference 10π units is ______.
