Advertisements
Advertisements
प्रश्न
Form the differential equation of the family of hyperbolas having foci on x-axis and centre at origin.
उत्तर
The equation of the family of hyperbolas with the centre at origin and foci along the x-axis is:
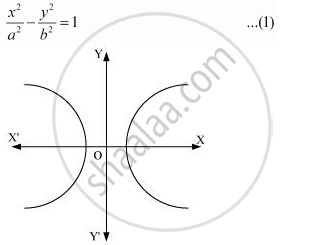
Differentiating both sides of equation (1) with respect to x, we get:

This is the required differential equation.
APPEARS IN
संबंधित प्रश्न
Form the differential equation representing the family of curves given by (x – a)2 + 2y2 = a2, where a is an arbitrary constant.
Form the differential equation of the family of curves represented by y2 = (x − c)3.
Form the differential equation corresponding to y = emx by eliminating m.
Form the differential equation from the following primitive where constants are arbitrary:
y = ax2 + bx + c
Find the differential equation of the family of curves y = Ae2x + Be−2x, where A and B are arbitrary constants.
Find the differential equation of the family of curves, x = A cos nt + B sin nt, where A and B are arbitrary constants.
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
x2 + y2 = a2
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
(x − a)2 − y2 = 1
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
y = ax3
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
y = eax
Show that y = bex + ce2x is a solution of the differential equation, \[\frac{d^2 y}{d x^2} - 3\frac{dy}{dx} + 2y = 0\]
Find one-parameter families of solution curves of the following differential equation:-
\[\frac{dy}{dx} + 3y = e^{mx}\], m is a given real number.
Find one-parameter families of solution curves of the following differential equation:-
\[\frac{dy}{dx} + y \cos x = e^{\sin x} \cos x\]
Find one-parameter families of solution curves of the following differential equation:-
\[x \log x\frac{dy}{dx} + y = 2 \log x\]
Write the order of the differential equation representing the family of curves y = ax + a3.
Form the differential equation representing the family of curves y = mx, where m is an arbitrary constant.
Form the differential equation of the family of ellipses having foci on y-axis and centre at the origin.
Find the area of the region bounded by the curves (x -1)2 + y2 = 1 and x2 + y2 = 1, using integration.
Form the differential equation representing the family of curves y = e2x (a + bx), where 'a' and 'b' are arbitrary constants.
Form the differential equation representing the family of curves y = A sin x, by eliminating the arbitrary constant A.
Find the differential equation of the family of curves y = Ae2x + B.e–2x.
Find the differential equation of the family of lines through the origin.
The differential equation representing the family of curves y = A sinx + B cosx is ______.
Find the equation of a curve passing through origin and satisfying the differential equation `(1 + x^2) "dy"/"dx" + 2xy` = 4x2
Form the differential equation by eliminating A and B in Ax2 + By2 = 1
Find the equation of a curve passing through (2, 1) if the slope of the tangent to the curve at any point (x, y) is `(x^2 + y^2)/(2xy)`.
Find the equation of the curve through the point (1, 0) if the slope of the tangent to the curve at any point (x, y) is `(y - 1)/(x^2 + x)`
Find the equation of a curve passing through origin if the slope of the tangent to the curve at any point (x, y) is equal to the square of the difference of the abcissa and ordinate of the point.
Family y = Ax + A3 of curves will correspond to a differential equation of order ______.
The differential equation representing the family of circles x2 + (y – a)2 = a2 will be of order two.
Find the equation of the curve at every point of which the tangent line has a slope of 2x:
The area above the x-axis and under the curve `y = sqrt(1/x - 1)` for `1/2 ≤ x ≤ 1` is:
Form the differential equation of family of circles having centre on y-axis and raduis 3 units
Form the differential equation of the family of hyperbola having foci on x-axis and centre at origin.
