Advertisements
Advertisements
प्रश्न
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 90 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
उत्तर
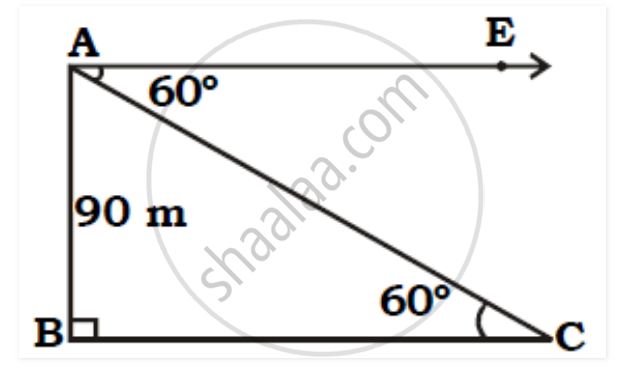
As shown in the figure, assume AB as the lighthouse and let A be the position of the observer and C be the position of the ship. Let the distance from the ship to the lighthouse be x.
Let AB be the height of the lighthouse,
∴ AB = 90 metres [Given]
The point 'C' be the position of the ship,
∴ ∠ ACB = 600
tan 600 = Opposite side of 600 / Adjacent side of 600
∴ tan 600 = AB / BC
∴ √3 = 90/BC
∴ BC = 90/√ 3
∴ BC = (90/√3)× √3/√3
∴ BC = 30√3
∴ BC = 30× 1.73
∴ BC = 51.9 m.
∴ The ship is 51.9 m away from the lighthouse.
APPEARS IN
संबंधित प्रश्न
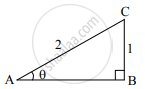
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
Two building are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 40 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car as an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill.
A TV tower stands vertically on a bank of a river/canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the river/canal.
Find the angle of elevation of the sum (sun's altitude) when the length of the shadow of a vertical pole is equal to its height.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.

Radii of the top and the base of a frustum of a cone are 5 cm and 2 cm respectively. Its height is 9 cm. Find its volume. (π = 3.14)
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
From the top of a lighthouse, the angle of depression of two ships on the opposite sides of it is observed to be 30° and 60°. If the height of the lighthouse is h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance between the ships is `(4"h")/sqrt(3)` m
From the top of a tree of height 13 m the angle of elevation and depression of the top and bottom of another tree are 45° and 30° respectively. Find the height of the second tree. `(sqrt(3) = 1.732)`
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
The angles of elevation of the top of a tower from two points distant s and t from its foot are complementary. Then the height of the tower is ____________.
There are two windows in a house. A window of the house is at a height of 1.5 m above the ground and the other window is 3 m vertically above the lower window. Ram and Shyam are sitting inside the two windows. At an instant, the angle of elevation of a balloon from these windows is observed as 45° and 30° respectively. Find the height of the balloon from the ground.
Lakshaman Jhula is located 5 kilometers north-east of the city of Rishikesh in the Indian state of Uttarakhand. The bridge connects the villages of Tapovan to Jonk. Tapovan is in Tehri Garhwal district, on the west bank of the river, while Jonk is in Pauri Garhwal district, on the east bank. Lakshman Jhula is a pedestrian bridge also used by motorbikes. It is a landmark of Rishikesh. A group of Class X students visited Rishikesh in Uttarakhand on a trip. They observed from a point (P) on a river bridge that the angles of depression of opposite banks of the river are 60° and 30° respectively. The height of the bridge is about 18 meters from the river. |
Based on the above information answer the following questions.
- Find the distance PA.
- Find the distance PB
- Find the width AB of the river.
[OR]
Find the height BQ if the angle of the elevation from P to Q be 30°.
Read the following passage and answer the questions given below.
|
Qutub Minar, located in South Delhi, India was built in the year 1193. It is 72 m high tower. Working on a school project, Charu and Daljeet visited the monument. They used trigonometry to find their distance from the tower. Observe the picture given below. Points C and D represent their positions on the ground in line with the base of tower, the angles of elevation of top of the tower (Point A) are 60° and 45° from points C and D respectively.
|
- Based on the above information, draw a well-labelled diagram.
- Find the distances CD, BC and BD. [use `sqrt(3)` = 1.73]
A person is standing at a distance of 50 m from a temple looking at its top. The angle of elevation is 45°. Find the height of the temple.
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?

