Advertisements
Advertisements
प्रश्न
If cosec θ = `(29)/(20)`, find the value of: `("sec" θ)/("tan" θ - "cosec" θ)`
उत्तर
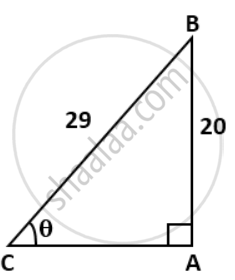
Consider ΔABC, where ∠A = 90°
⇒ cosec θ = `"Hypotenuse"/"Perpendicular" = "BC"/"AB" = (29)/(20)`
By Pythagoras theorem,
BC2 = AB2 + AC2
⇒ AC2 = BC2 - AB2
= 292 - 202
= 841 - 400
= 441
⇒ AC = 21
Now,
sec θ = `"Hypotenuse"/"Base" = "BC"/"AC" = (29)/(21)`
tan θ = `"Perpendicular"/"Base" = "AB"/"AC" = (20)/(21)`
⇒ cot θ = `(1)/"tan θ " = (21)/(20)`
`"sec θ"/("tan" θ - "cosec" θ")`
= `(29/21)/(20/21 - 29/20)`
= `(29/21)/(-209/420)`
= `(29)/(21) xx (-420)/(209)`
= `(-580)/(209)`.
APPEARS IN
संबंधित प्रश्न
If cot θ = 2 find all the values of all T-ratios of θ .
If sec `theta = 17/8 ` verify that `((3-4sin^2theta)/(4 cos^2theta -3))=((3-tan^2theta)/(1-tan^2theta))`
If ∠A and ∠B are acute angles such that sin A = Sin B prove that ∠A = ∠B.
Evaluate:
`(sin^2 30^0 + 4 cot^2 45^0-sec^2 60^0)(cosec^2 45^0 sec^2 30^0)`
If A = 600 and B = 300, verify that:
(i) sin (A + B) = sin A cos B + cos A sin B
If A = 600 and B = 300, verify that:
cos (A + B) = cos A cos B - sin A sin B
Given: 4 cot A = 3
find :
(i) sin A
(ii) sec A
(iii) cosec2A - cot2A.
Given: sin θ = `p/q`.
Find cos θ + sin θ in terms of p and q.
In rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.
If 5 cos θ = 3, evaluate : `(co secθ – cot θ)/(co secθ + cot θ)`
