Advertisements
Advertisements
प्रश्न
Let A and B be sets. Show that f: A × B → B × A such that (a, b) = (b, a) is bijective function.
उत्तर
f: A × B → B × A is defined as f(a, b) = (b, a).
Let `(a_1, b_1), (a_2, b_2) in A xx B " such that " f(a_1, b_1) = (a_2, b_2)`
`=> (b_1 , a_1) = (b_2, a_2)`
`=> b_1 = b_2 and a_1 = a_2`
`=> (a_1, b_1) =(a_2, b_2)`
∴ f is injective.
Now, let (b, a) ∈ B × A be any element.
Then, there exists (a, b) ∈A × B such that f(a, b) = (b, a). [By definition of f]
∴ f is bijective.
APPEARS IN
संबंधित प्रश्न
Prove that the greatest integer function f: R → R, given by f(x) = [x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.
Show that the modulus function f: R → R given by f(x) = |x| is neither one-one nor onto, where |x| is x, if x is positive or 0 and |x| is − x if x is negative.
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one.
Let f: N → N be defined by f(n) = `{((n+1)/2, ",if n is odd"),(n/2,",n is even"):}` for all n ∈ N.
State whether the function f is bijective. Justify your answer.
Give an example of a function which is not one-one but onto ?
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = sinx
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = 1 + x2
Show that the function f : R − {3} → R − {2} given by f(x) = `(x-2)/(x-3)` is a bijection.
Let A = {1, 2, 3}. Write all one-one from A to itself.
Give examples of two one-one functions f1 and f2 from R to R, such that f1 + f2 : R → R. defined by (f1 + f2) (x) = f1 (x) + f2 (x) is not one-one.
Give examples of two functions f : N → Z and g : Z → Z, such that gof is injective but gis not injective.
Let f(x) = x2 + x + 1 and g(x) = sin x. Show that fog ≠ gof.
Let A = R - {3} and B = R - {1}. Consider the function f : A → B defined by f(x) = `(x-2)/(x-3).`Show that f is one-one and onto and hence find f-1.
[CBSE 2012, 2014]
Which one of the following graphs represents a function?
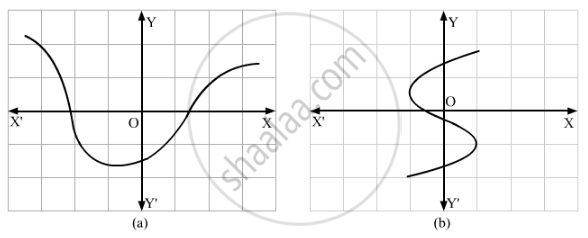
If A = {1, 2, 3} and B = {a, b}, write the total number of functions from A to B.
If f : R → R, g : R → are given by f(x) = (x + 1)2 and g(x) = x2 + 1, then write the value of fog (−3).
Let \[f : \left[ - \frac{\pi}{2}, \frac{\pi}{2} \right] \to\] A be defined by f(x) = sin x. If f is a bijection, write set A.
Let
\[A = \left\{ x : - 1 \leq x \leq 1 \right\} \text{and} f : A \to \text{A such that f}\left( x \right) = x|x|\]
If the function\[f : R \to \text{A given by} f\left( x \right) = \frac{x^2}{x^2 + 1}\] is a surjection, then A =
Let
\[f : R - \left\{ n \right\} \to R\]
\[f : Z \to Z\] be given by
` f (x) = {(x/2, ", if x is even" ) ,(0 , ", if x is odd "):}`
Then, f is
If \[g \left( f \left( x \right) \right) = \left| \sin x \right| \text{and} f \left( g \left( x \right) \right) = \left( \sin \sqrt{x} \right)^2 , \text{then}\]
Let \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] Then, for what value of α is \[f \left( f\left( x \right) \right) = x?\]
If \[f : R \to R\] is given by \[f\left( x \right) = x^3 + 3, \text{then} f^{- 1} \left( x \right)\] is equal to
Let \[f\left(x\right) = x^3\] be a function with domain {0, 1, 2, 3}. Then domain of \[f^{-1}\] is ______.
If A = {a, b, c, d} and f = {a, b), (b, d), (c, a), (d, c)}, show that f is one-one from A onto A. Find f–1
Let f: R → R be the function defined by f(x) = 2x – 3 ∀ x ∈ R. write f–1
If f: R → R is defined by f(x) = x2 – 3x + 2, write f(f (x))
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
f(x) = `x/2`
Let f: `[2, oo)` → R be the function defined by f(x) = x2 – 4x + 5, then the range of f is ______.
The smallest integer function f(x) = [x] is ____________.
Let f : R → R be a function defined by f(x) `= ("e"^abs"x" - "e"^-"x")/("e"^"x" + "e"^-"x")` then f(x) is
Let R be a relation on the set L of lines defined by l1 R l2 if l1 is perpendicular to l2, then relation R is ____________.
Prove that the function f is surjective, where f: N → N such that `f(n) = {{:((n + 1)/2",", if "n is odd"),(n/2",", if "n is even"):}` Is the function injective? Justify your answer.
The graph of the function y = f(x) is symmetrical about the line x = 2, then ______.
Let a function `f: N rightarrow N` be defined by
f(n) = `{:[(2n",", n = 2"," 4"," 6"," 8","......),(n - 1",", n = 3"," 7"," 11"," 15","......),((n + 1)/2",", n = 1"," 5"," 9"," 13","......):}`
then f is ______.
Let S = {1, 2, 3, 4, 5, 6, 7}. Then the number of possible functions f: S `rightarrow` S such that f(m.n) = f(m).f(n) for every m, n ∈ S and m.n ∈ S is equal to ______.
