Advertisements
Advertisements
प्रश्न
निम्न समस्या में रैखिक समीकरण के युग्म बनाइए और उसके ग्राफीय विधि से हल ज्ञात कीजिए।
कक्षा X के 10 विद्यार्थियों ने एक गणित की पहेली प्रतियोगिता में भाग लिया। यदि लड़कियों की संख्या लड़कों की संख्या से 4 अधिक हो, तो प्रतियोगिता में भाग लिए लड़कों और लड़कियों की संख्या ज्ञात कीजिए।
Advertisements
उत्तर १
मान लीजिए लड़कों की संख्या x है और लड़कियों की संख्या y है।
तब बनने वाले समीकरण हैं
x + y = 10 ...(1) और y = x + 4 ...(2)
आइए समीकरणों में से प्रत्येक के लिए दो हल ज्ञात करके समीकरण (1) और (2) के ग्राफ बनाएं।
समीकरणों के हल दिए गए हैं।
x + y = 10 ⇒ y = 10 – x
| x | 0 | 8 |
| y | 10 | 2 |
| Points | A | B |
y = x + 4
| x | 0 | 1 | 3 |
| y | 4 | 5 | 7 |
| Points | C | D | E |
इन बिंदुओं को प्लॉट करके हम समीकरणों को दर्शाने के लिए उनसे गुजरने वाली रेखाएँ AB और CE खींचते हैं। दो रेखाएँ AB और Ce बिंदु E (3, 7) पर प्रतिच्छेद करती हैं। इसलिए, x = 3 और y = 7 रैखिक समीकरणों की जोड़ी का अभीष्ट हल है।
यानी लड़कों की संख्या = 3
लड़कियों की संख्या = 7
सत्यापन:
(1) में x = 3 और y = 7 रखने पर, हमें मिलता है
बाएं पक्ष = 3 + 7 = 10 = दाएँ पक्ष, (1) सत्यापित है।
(2) में x = 3 और y = 7 रखने पर, हमें मिलता है
7 = 3 + 4 = 7, (2) सत्यापित है।
इसलिए, दोनों समीकरण संतुष्ट हैं।
उत्तर २
माना लड़कियों की संख्या = x
तथा लड़कों की संख्या = y
प्रश्नानुसार,
लड़के और लड़कियाँ की कुल संख्या 10 है।
इसलिए, x + y = 10 ...(1)
लड़कों से लड़कियाँ 4 अधिक हैं।
इसलिए, x - y = 4 ...(2)
समी. (1) के लिए तालिका
x + y = 10
⇒ x = 10 - y
| x | 5 | 6 | 7 |
| y | 5 | 4 | 3 |
समी. (2) के लिए तालिका
x - y = 4
⇒ x = 4 + y
| x | 5 | 6 | 7 |
| y | 1 | 2 | 3 |
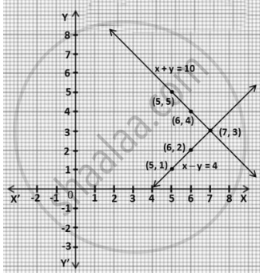
ग्राफीय विधि से हल के लिए हम जब बने ग्राफ को देखते हैं तो पाते हैं कि बिंदु (7, 3) दिए गए समीकरण के लिए प्रतिच्छेदन बिंदु है जो कि रैखिक समीकरण युग्म का उभयनिष्ठ हल है।
इसलिए, लड़कियों कि संख्या = 7 और लड़कों की संख्या = 3 है।
APPEARS IN
संबंधित प्रश्न
निम्न समस्या में रैखिक समीकरण के युग्म बनाइए और उनके ग्राफीय विधि से हल ज्ञात कीजिए।
5 पेंसिल तथा 7 कलमों का कुल मूल्य ₹ 50 है, जबकि 7 पेंसिल तथा 5 कलमों का कुल मूल्य ₹ 46 है। एक पेंसिल का मूल्य तथा एक कलम मूल्य ज्ञात कीजिए।
अनुपातों `bb(a_1/a_2, b_1/b_2)` और `bb(c_1/c_2)` की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरण के युग्म संगत हैं या असंगत:
3x + 2y = 5; 2x - 3y = 7
निम्न रैखिक समीकरणों के युग्मों में से कौन से युग्म संगत/असंगत हैं, यदि संगत हैं तो ग्राफीय विधि से हल ज्ञात कीजिए।
x + y = 5, 2x + 2y = 10
एक रैखिक समीकरण 2x + 3y - 8 = 0 दी गई है। दो चरों में एक ऐसी और रैखिक समीकरण लिखिए ताकि प्राप्त युग्म का ज्यामितीय निरूपण जैसा कि
- प्रतिच्छेद करती रेखाएँ हों।
- समांतर रेखाएँ हों।
- संपाती रेखाएँ हों।
क्या समीकरणों के निम्नलिखित युग्म का कोई हल नहीं है? अपने उत्तर का औचित्य दीजिए।
x = 2y, y = 2x
क्या निम्नलिखित समीकरण संपाती रेखाओं का एक युग्म निरूपित करती है? अपने उत्तर का औचित्य दीजिए।
–2x – 3y = 1, 6y + 4x = – 2
x = 7 द्वारा निरूपित रेखा x अक्ष के समांतर है औचित्य के साथ उत्तर दीजिए कि यह सत्य है या असत्य।
रैखिक समीकरण x + y = 2 और 2x – y = 1 के युग्म के हल को निरूपित करने वाले बिंदु से होकर जाने वाली एक रेखा की समीकरण ज्ञात कीजिए। हम ऐसी कितनी रेखाएँ ज्ञात कर सकते हैं?
निम्नलिखित समीकरण-युग्म को आलेखीय रूप से हल कीजिए:
2x + y = 6, 2x – y + 2 = 0
उन दो त्रिभुजों के क्षेत्रफलों का अनुपात ज्ञात कीजिए, जो इन समीकरणों को निरूपित करने वाली रेखाओं द्वारा क्रमश: x-अक्ष और y-अक्ष द्वारा बनाए जाते हैं।
λ के किस (किन) मान (मानों) के लिए रैखिक समीकरण-युग्म
λx + y = λ2
x + λy = 1
दो चरों वाले रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होंगे?
