Advertisements
Advertisements
प्रश्न
प्रथम चतुर्थांश में ऐसे वृत्तों के कुल का अवकल समीकरण ज्ञात कीजिए जो निर्देशांक अक्षों को स्पर्श करते हैं।
उत्तर
वह वृत्तों के कुल का समीकरण जो निर्देशांक अक्षों को स्पर्श करें
(x – a)2 + (y – a)2 = a2 …(1)
x के सापेक्ष अवकलन करने पर
2(x - a) + 2(y - a)`"dy"/"dx" = 0`
या x - a + (y - a)p = 0 जबकि p = `"dy"/"dx"`
⇒ x + py - a(1 + p) = 0
`therefore "a" = (x + "py")/(1 + "p")`
∴ `x - "a" = x - (x + "py")/(1 + "p")`
∴ `= (x + "p"x - x - "py")/(1 + "p")`
`= ((x - "y")"p")/(1 + "p")`
`"y - a" = "y" - (x + "py")/(1 + "p")`
`= ("y" + "py" - x - "py")/(1 + "p")`
`= ("y - x")/(1 + "p")`
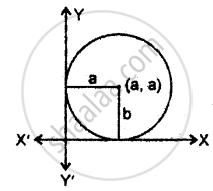
a, x - a, y - a का मान समीकरण (1) में रखने पर,
`(("x - y")^2 "p"^2)/(1 + "p")^2 + ("y - x")^2/(1 + "p")^2 = (x + "py")^2/(1 + "p")^2`
`=> (x - "y")^2 "p"^2 + (x - "y")^2 = (x + "py")^2`
या (x - y)2 (1 + p2) = (x + py)2
∴ अभीष्ट अवकल समीकरण,
`(x - "y")^2 [1 + ("dy"/"dx")^2] = [x + "y""dy"/"dx"]^2`
APPEARS IN
संबंधित प्रश्न
नीचे दिए गए प्रश्न में स्वेच्छ अचरों a तथा b को विलुप्त करते हुए दिए हुए वक्रों के कुल को निरूपित करने वाला अवकल समीकरण ज्ञात कीजिए।
`"x"/"a" + "y"/"b" = 1`
नीचे दिए गए प्रश्न में, स्वेच्छ अचरों a तथा b को विलुप्त करते हुए दिए हुए वक्रों के कुल को निरूपित करने वाला अवकल समीकरण ज्ञात कीजिए।
y2 = a (b2 - x2)
नीचे दिए गए प्रश्न में स्वेच्छ अचरों a तथा b को विलुप्त करते हुए दिए हुए वक्रों के कुल को निरूपित करने वाला अवकल समीकरण ज्ञात कीजिए।
y = ae3x + be-2x
नीचे दिए गए प्रश्न में स्वेच्छ अचरों a तथा b को विलुप्त करते हुए दिए हुए वक्रों के कुल को निरूपित करने वाला अवकल समीकरण ज्ञात कीजिए।
y = e2x (a + bx)
y - अक्ष को मूल बिंदु पर स्पर्श करने वाले वृत्तों के कुल का अवकल समीकरण ज्ञात कीजिए।
ऐसे परवलयों के कुल का अवकल समीकरण निर्मित कीजिए जिनका शीर्ष मूल बिंदु पर है और जिनका अक्ष धनात्मक y - अक्ष की दिशा में है।
ऐसे दीर्घवृत्तों के कुल का अवकल समीकरण ज्ञात कीजिए जिनकी नाभियाँ y - अक्ष पर हैं तथा जिनका केंद्र मूल बिंदु है।
ऐसे अतिपरवलयों के कुल का अवकल समीकरण ज्ञात कीजिए जिनकी नाभियाँ x-अक्ष पर हैं तथा जिनका केंद्र मूल बिंदु है।
ऐसे वृत्तों के कुल का अवकल समीकरण ज्ञात कीजिए जिनका केंद्र y-अक्ष पर है और जिनकी त्रिज्या 3 इकाई है।
निम्नलिखित अवकल समीकरणों में से किस समीकरण का व्यापक हल y = c1 ex + c2 e-x है?
निम्नलिखित समीकरणों में से किस समीकरण का एक विशिष्ट हल y = x है?
(x – a)2 + 2y2 = a2 द्वारा निरूपित वक्रों के कुल का अवकल समी० निर्मित कीजिए जहाँ a एक स्वेच्छ अचर है।
सिद्ध कीजिए कि x2 – y2 = c (x2 + y2)2 जहाँ c एक प्राचल है, अवकल समीकरण (x3 – 3x y2)dx = (y3 – 3x2y) dy का व्यापक हल है।
अवकल समीकरण `dy/dx + sqrt((1 - y^2)/(1 - x^2))`= 0, जबकि x ≠ 1 का व्यापक हल ज्ञात कीजिए।
बिंदु `(0, π/4)` से गुजरने वाले एक ऐसे वक्र का समीकरण ज्ञात कीजिए जिसका अवकल समीकरण sin x cos y dx + cos x sin y dy = 0 है।
किसी गाँव की जनसंख्या की वृद्धि की दर किसी भी समय उस गाँव के निवासियों की संख्या के समानुपाती है। यदि सन् 1999 में गाँव की जनसंख्या 20,000 थी और सन् 2004 में 25,000 थी तो ज्ञात कीजिए कि सन् 2009 में गाँव की जनसंख्या क्या होगी?
`dx/dy + P_1 x = Q_1` के रूप वाले अवकल समीकरण का व्यापक हल है:
अवकल समीकरण exdy + (yex + 2x) dx = 0 का व्यापक हल है:
