Advertisements
Advertisements
प्रश्न
Show that there can be no net charge in a region in which the electric field is uniform at all points.
उत्तर
It is given that the electric field is uniform. If we consider a surface perpendicular to the electric field, we find that it is an equipotential surface. Hence, if a test charge is introduced on the surface, then work done will be zero in moving the test charge on it.
But if there is some net charge in this region, the test charge introduced on the surface will experience a force due to this charge. This force has a component parallel to the surface; thus, work has to be done in moving this test charge. Thus, the surface cannot be said to be equipotential. This implies that the net charge in the region with uniform electric field is zero.
APPEARS IN
संबंधित प्रश्न
Plot a graph showing the variation of resistivity of a conductor with temperature.
A charge Q is uniformly distributed over a rod of length l. Consider a hypothetical cube of edge l with the centre of the cube at one end of the rod. Find the minimum possible flux of the electric field through the entire surface of the cube.
The electric field in a region is given by
`vec"E"= 3/5"E"_0 vec"i" + 4/5 "E"_0 vec "i" "with" " E"_0 = 2.0 xx 10^3 "N""C"^-1.`
Find the flux of this field through a rectangular surface of area 0⋅2 m2 parallel to the y-z plane.
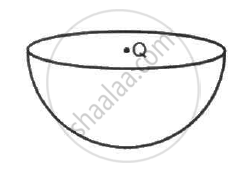
A charge Q is placed at the centre of an imaginary hemispherical surface. Using symmetry arguments and Gauss's Law, find the flux of the electric field due to this charge through the surface of the hemisphere in the following figure.
The radius of a gold nucleus (Z = 79) is about 7.0 × 10-10 m. Assume that the positive charge is distributed uniformly throughout the nuclear volume. Find the strength of the electric field at (a) the surface of the nucleus and (b) at the middle point of a radius. Remembering that gold is a conductor, is it justified to assume that the positive charge is uniformly distributed over the entire volume of the nucleus and does not come to the outer surface?
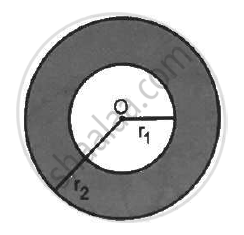
A charge Q is distributed uniformly within the material of a hollow sphere of inner and outer radii r1 and r2 (see the figure). Find the electric field at a point P at a distance x away from the centre for r1 < x < r. Draw a rough graph showing the electric field as a function of x for 0 < x < 2r2 (see the figure).
A non-conducting sheet of large surface area and thickness d contains a uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane. Draw a qualitative graph of E against x for 0 < x < d.
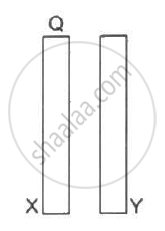
Two conducting plates X and Y, each with a large surface area A (on one side), are placed parallel to each other, as shown in the following figure . Plate X is given a charge Q,whereas the other is kept neutral. Find (a) the surface charge density at the inner surface of plate X (b) the electric field at a point to the left of the plates (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.
Consider a circular ring of radius r, uniformly charged with linear charge density λ. Find the electric potential at a point on the axis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
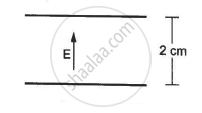
An electric field of magnitude 1000 NC−1 is produced between two parallel plates with a separation of 2.0 cm, as shown in the figure. (a) What is the potential difference between the plates? (b) With what minimum speed should an electron be projected from the lower place in the direction of the field, so that it may reach the upper plate? (c) Suppose the electron is projected from the lower place with the speed calculated in part (b). The direction of projection makes an angle of 60° with the field. Find the maximum height reached by the electron.
Answer the following question.
Prove that the average energy density of the oscillating electric field is equal to that of the oscillating magnetic field.
A simple pendulum consists of a small sphere of mass m suspended by a thread of length l. The sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically downwards. Find the period of oscillation of the pendulum due to the electrostatic force acting on the sphere, neglecting the effect of the gravitational force.
Electric field at a point is defined as ______.
When a comb rubbed with dry hair attracts pieces of paper. This is because the ______.
