Advertisements
Advertisements
प्रश्न
The monthly consumption of electricity (in units) of some families of a locality is given in the following frequency distribution:
| Monthly Consumption (in units) | 140 – 160 | 160 – 180 | 180 – 200 | 200 – 220 | 220 – 240 | 240 – 260 | 260 - 280 |
| Number of Families | 3 | 8 | 15 | 40 | 50 | 30 | 10 |
Prepare a ‘more than type’ ogive for the given frequency distribution.
उत्तर
The frequency distribution table of more than type is as follows:
| Height (in cm) (lower class limit) | Cumulative frequency (cf) |
| More than 140 | 3 + 153 = 156 |
| More than 160 | 8 + 145 = 153 |
| More than 180 | 15 + 130 = 145 |
| More than 200 | 40 + 90 = 130 |
| More than 220 | 50 + 40 = 90 |
| More than 240 | 30 + 10 = 40 |
| More than 260 | 10 |
Taking the lower class limits of on x-axis and their respective cumulative frequencies ony-axis, its ogive can be drawn as follows: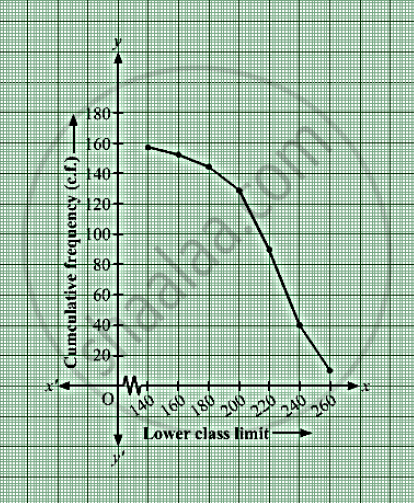
APPEARS IN
संबंधित प्रश्न
The following distribution gives the daily income of 50 workers of a factory.
| Daily income (in Rs | 100 − 120 | 120 − 140 | 140 − 160 | 160 − 180 | 180 − 200 |
| Number of workers | 12 | 14 | 8 | 6 | 10 |
Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.
Find the median of the following data by making a ‘less than ogive’.
| Marks | 0 - 10 | 10-20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 | 70 - 80 | 80-90 | 90-100 |
| Number of Students | 5 | 3 | 4 | 3 | 3 | 4 | 7 | 9 | 7 | 8 |
Write the median class of the following distribution:
| Class | 0 – 10 | 10 -20 | 20- 30 | 30- 40 | 40-50 | 50- 60 | 60- 70 |
| Frequency | 4 | 4 | 8 | 10 | 12 | 8 | 4 |
If \[u_i = \frac{x_i - 25}{10}, \Sigma f_i u_i = 20, \Sigma f_i = 100, \text { then }\]`overlineX`
Consider the following frequency distributions
| Class | 65 - 85 | 85 - 105 | 105 - 125 | 125 - 145 | 145 - 165 | 165 - 185 | 185-205 |
| Frequency | 4 | 5 | 13 | 20 | 14 | 7 | 4 |
The difference of the upper limit of the median class and the lower limit of the modal class is?
The arithmetic mean of the following frequency distribution is 53. Find the value of k.
| Class | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| Frequency | 12 | 15 | 32 | k | 13 |
The marks obtained by 100 students of a class in an examination are given below.
| Mark | No. of Student |
| 0 - 5 | 2 |
| 5 - 10 | 5 |
| 10 - 15 | 6 |
| 15 - 20 | 8 |
| 20 - 25 | 10 |
| 25 - 30 | 25 |
| 30 - 35 | 20 |
| 35 - 40 | 18 |
| 40 - 45 | 4 |
| 45 - 50 | 2 |
Draw 'a less than' type cumulative frequency curves (ogive). Hence find the median.
For the following distribution:
| C.I. | 0 - 5 | 6 - 11 | 12 - 17 | 18 - 23 | 24 - 29 |
| f | 13 | 10 | 15 | 8 | 11 |
the upper limit of the median class is?
The following is the distribution of weights (in kg) of 40 persons:
| Weight (in kg) | 40 – 45 | 45 – 50 | 50 – 55 | 55 – 60 | 60 – 65 | 65 – 70 | 70 – 75 | 75 – 80 |
| Number of persons | 4 | 4 | 13 | 5 | 6 | 5 | 2 | 1 |
Construct a cumulative frequency distribution (of the less than type) table for the data above.
The following table shows the cumulative frequency distribution of marks of 800 students in an examination:
| Marks | Number of students |
| Below 10 | 10 |
| Below 20 | 50 |
| Below 30 | 130 |
| Below 40 | 270 |
| Below 50 | 440 |
| Below 60 | 570 |
| Below 70 | 670 |
| Below 80 | 740 |
| Below 90 | 780 |
| Below 100 | 800 |
Construct a frequency distribution table for the data above.
