Advertisements
Advertisements
प्रश्न
The following table gives the production yield per hectare of wheat of 100 farms of a village.
| Production Yield (kg/ha) | 50 –55 | 55 –60 | 60 –65 | 65- 70 | 70 – 75 | 75 80 |
| Number of farms | 2 | 8 | 12 | 24 | 238 | 16 |
Change the distribution to a ‘more than type’ distribution and draw its ogive. Using ogive, find the median of the given data.
उत्तर
The frequency distribution table of more than type is as follows:
| Production yield (kg/ha) (lower class limits) | Cumulative frequency (cf) |
| More than 50 | 2 + 98 = 100 |
| More than 55 | 8 + 90 = 98 |
| More than 60 | 12 + 78 = 90 |
| More than 65 | 24 + 54 = 78 |
| More than 70 | 38 + 16 = 54 |
| More than 75 | 16 |
Taking the lower class limits on x-axis and their respective cumulative on y-axis, its ogive can be drawn as follows
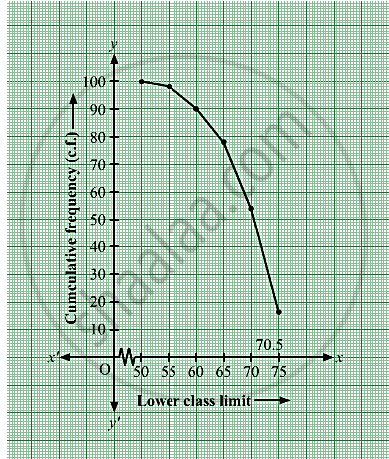
Here, N = 100 ⇒ `N/2 = 50.`
Mark the point A whose ordinate is 50 and its x-coordinate is 70.5.
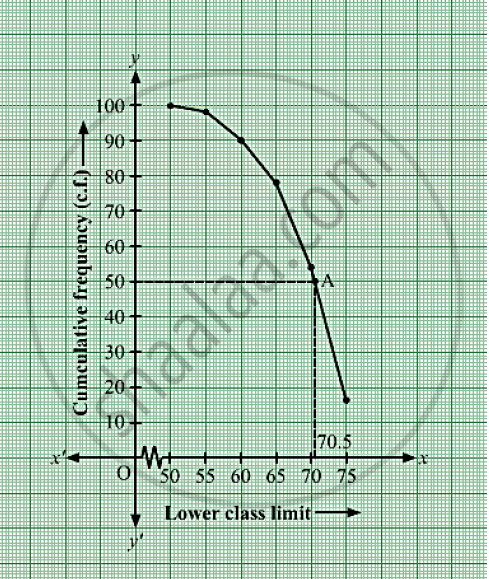
Thus, median of the data is 70.5.
APPEARS IN
संबंधित प्रश्न
During the medical check-up of 35 students of a class, their weights were recorded as follows:
| Weight (in kg | Number of students |
| Less than 38 | 0 |
| Less than 40 | 3 |
| Less than 42 | 5 |
| Less than 44 | 9 |
| Less than 46 | 14 |
| Less than 48 | 28 |
| Less than 50 | 32 |
| Less than 52 | 35 |
Draw a less than type ogive for the given data. Hence obtain the median weight from the graph verify the result by using the formula.
The monthly profits (in Rs.) of 100 shops are distributed as follows:
| Profits per shop: | 0 - 50 | 50 - 100 | 100 - 150 | 150 - 200 | 200 - 250 | 250 - 300 |
| No. of shops: | 12 | 18 | 27 | 20 | 17 | 6 |
Draw the frequency polygon for it.
Write the median class for the following frequency distribution:
| Class-interval: | 0−10 | 10−20 | 20−30 | 30−40 | 40−50 | 50−60 | 60−70 | 70−80 |
| Frequency: | 5 | 8 | 7 | 12 | 28 | 20 | 10 | 10 |
For a frequency distribution, mean, median and mode are connected by the relation
The mode of a frequency distribution can be determined graphically from ______.
Consider the following frequency distribution :
| Class: | 0-5 | 6-11 | 12-17 | 18-23 | 24-29 |
| Frequency: | 13 | 10 | 15 | 8 | 11 |
The upper limit of the median class is
Find the mode of the following frequency distribution.
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 |
| Frequency | 8 | 10 | 10 | 16 | 12 | 6 | 7 |
The marks obtained by 100 students of a class in an examination are given below.
| Mark | No. of Student |
| 0 - 5 | 2 |
| 5 - 10 | 5 |
| 10 - 15 | 6 |
| 15 - 20 | 8 |
| 20 - 25 | 10 |
| 25 - 30 | 25 |
| 30 - 35 | 20 |
| 35 - 40 | 18 |
| 40 - 45 | 4 |
| 45 - 50 | 2 |
Draw 'a less than' type cumulative frequency curves (ogive). Hence find the median.
The following is the distribution of weights (in kg) of 40 persons:
| Weight (in kg) | 40 – 45 | 45 – 50 | 50 – 55 | 55 – 60 | 60 – 65 | 65 – 70 | 70 – 75 | 75 – 80 |
| Number of persons | 4 | 4 | 13 | 5 | 6 | 5 | 2 | 1 |
Construct a cumulative frequency distribution (of the less than type) table for the data above.
Find the unknown entries a, b, c, d, e, f in the following distribution of heights of students in a class:
| Height (in cm) |
Frequency | Cumulative frequency |
| 150 – 155 | 12 | a |
| 155 – 160 | b | 25 |
| 160 – 165 | 10 | c |
| 165 – 170 | d | 43 |
| 170 – 175 | e | 48 |
| 175 – 180 | 2 | f |
| Total | 50 |
