Advertisements
Advertisements
प्रश्न
The following table gives the production yield per hectare of wheat of 100 farms of a village.
| Production Yield (kg/ha) | 50 –55 | 55 –60 | 60 –65 | 65- 70 | 70 – 75 | 75 80 |
| Number of farms | 2 | 8 | 12 | 24 | 238 | 16 |
Change the distribution to a ‘more than type’ distribution and draw its ogive. Using ogive, find the median of the given data.
उत्तर
The frequency distribution table of more than type is as follows:
| Production yield (kg/ha) (lower class limits) | Cumulative frequency (cf) |
| More than 50 | 2 + 98 = 100 |
| More than 55 | 8 + 90 = 98 |
| More than 60 | 12 + 78 = 90 |
| More than 65 | 24 + 54 = 78 |
| More than 70 | 38 + 16 = 54 |
| More than 75 | 16 |
Taking the lower class limits on x-axis and their respective cumulative on y-axis, its ogive can be drawn as follows
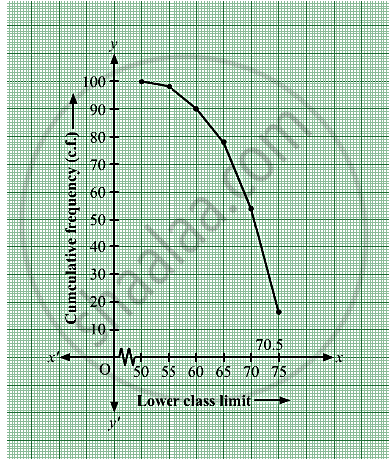
Here, N = 100 ⇒ `N/2 = 50.`
Mark the point A whose ordinate is 50 and its x-coordinate is 70.5.
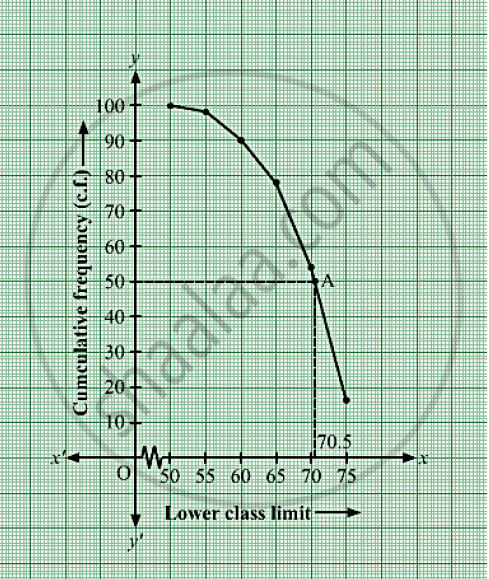
Thus, median of the data is 70.5.
APPEARS IN
संबंधित प्रश्न
The following table gives production yield per hectare of wheat of 100 farms of a village.
| Production yield (in kg/ha) | 50 − 55 | 55 − 60 | 60 − 65 | 65 − 70 | 70 − 75 | 75 − 80 |
| Number of farms | 2 | 8 | 12 | 24 | 38 | 16 |
Change the distribution to a more than type distribution and draw ogive.
The given distribution shows the number of wickets taken by the bowlers in one-day international cricket matches:
| Number of Wickets | Less than 15 | Less than 30 | Less than 45 | Less than 60 | Less than 75 | Less than 90 | Less than 105 | Less than 120 |
| Number of bowlers | 2 | 5 | 9 | 17 | 39 | 54 | 70 | 80 |
Draw a ‘less than type’ ogive from the above data. Find the median.
The marks obtained by 100 students of a class in an examination are given below:
| Marks | Number of students |
| 0 – 5 | 2 |
| 5 – 10 | 5 |
| 10 – 15 | 6 |
| 15 – 20 | 8 |
| 20 – 25 | 10 |
| 25 – 30 | 25 |
| 30 – 35 | 20 |
| 35 – 40 | 18 |
| 40 – 45 | 4 |
| 45 – 50 | 2 |
Draw cumulative frequency curves by using (i) ‘less than’ series and (ii) ‘more than’ series.Hence, find the median.
What is the lower limit of the modal class of the following frequency distribution?
| Age (in years) | 0 - 10 | 10- 20 | 20 -30 | 30 – 40 | 40 –50 | 50 – 60 |
| Number of patients | 16 | 13 | 6 | 11 | 27 | 18 |
The following are the ages of 300 patients getting medical treatment in a hospital on a particular day:
| Age (in years) | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 -70 |
| Number of patients | 6 | 42 | 55 | 70 | 53 | 20 |
Form a ‘less than type’ cumulative frequency distribution.
Write the modal class for the following frequency distribution:
| Class-interval: | 10−15 | 15−20 | 20−25 | 25−30 | 30−35 | 35−40 |
| Frequency: | 30 | 35 | 75 | 40 | 30 | 15 |
Consider the following frequency distribution :
| Class: | 0-5 | 6-11 | 12-17 | 18-23 | 24-29 |
| Frequency: | 13 | 10 | 15 | 8 | 11 |
The upper limit of the median class is
For one term, absentee record of students is given below. If mean is 15.5, then the missing frequencies x and y are.
| Number of days | 0 - 5 | 5 - 10 | 10 - 15 | 15 - 20 | 20 - 25 | 25 - 30 | 30 - 35 | 35 - 40 | TOTAL |
| Total Number of students | 15 | 16 | x | 8 | y | 8 | 6 | 4 | 70 |
The following is the distribution of weights (in kg) of 40 persons:
| Weight (in kg) | 40 – 45 | 45 – 50 | 50 – 55 | 55 – 60 | 60 – 65 | 65 – 70 | 70 – 75 | 75 – 80 |
| Number of persons | 4 | 4 | 13 | 5 | 6 | 5 | 2 | 1 |
Construct a cumulative frequency distribution (of the less than type) table for the data above.
Form the frequency distribution table from the following data:
| Marks (out of 90) | Number of candidates |
| More than or equal to 80 | 4 |
| More than or equal to 70 | 6 |
| More than or equal to 60 | 11 |
| More than or equal to 50 | 17 |
| More than or equal to 40 | 23 |
| More than or equal to 30 | 27 |
| More than or equal to 20 | 30 |
| More than or equal to 10 | 32 |
| More than or equal to 0 | 34 |
