Advertisements
Advertisements
प्रश्न
Two ships leave a port at the same time. One goes 24 km/hr in the direction N 38° E and other travels 32 km/hr in the direction S 52° E. Find the distance between the ships at the end of 3 hrs.
उत्तर
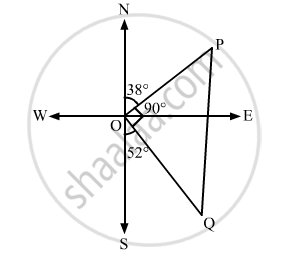
\[\text{ After three hours, let the ships be at P and Q respectively } . \]
\[\text{ Then }, \]
\[OP = 24 \times 3 = 72 km \text{ and } OQ = 32 \times 3 = 96 km\]
\[\text{ From figure, we have }\]
\[\angle POQ = 180° - \angle NOP - \angle SOQ\]
\[ = 180° - 38° - 52° \]
\[ = 90° \]
\[\text{ Now }, \]
\[\text{ Since OPQ is a right angled triangle }\]
\[ \therefore P Q^2 = O P^2 + O Q^2 \]
\[ \Rightarrow P Q^2 = {72}^2 + {96}^2 \]
\[ \Rightarrow P Q^2 = 5184 + 9216\]
\[ \Rightarrow P Q^2 = 14400\]
\[ \Rightarrow PQ = \sqrt{14400} = 120 km\]
\[\text{Hence, the distance between the ships after 3 hours is 120 km} .\]
APPEARS IN
संबंधित प्रश्न
If in ∆ABC, ∠A = 45°, ∠B = 60° and ∠C = 75°, find the ratio of its sides.
In triangle ABC, prove the following:
\[\left( a - b \right) \cos \frac{C}{2} = c \sin \left( \frac{A - B}{2} \right)\]
In triangle ABC, prove the following:
In triangle ABC, prove the following:
In any triangle ABC, prove the following:
In triangle ABC, prove the following:
In triangle ABC, prove the following:
In triangle ABC, prove the following:
In triangle ABC, prove the following:
In ∆ABC, prove that: \[a \sin\frac{A}{2} \sin \left( \frac{B - C}{2} \right) + b \sin \frac{B}{2} \sin \left( \frac{C - A}{2} \right) + c \sin \frac{C}{2} \sin \left( \frac{A - B}{2} \right) = 0\]
In ∆ABC, prove that \[a \left( \cos C - \cos B \right) = 2 \left( b - c \right) \cos^2 \frac{A}{2} .\]
In ∆ABC, prove that if θ be any angle, then b cosθ = c cos (A − θ) + a cos (C + θ).
In ∆ABC, if sin2 A + sin2 B = sin2 C. show that the triangle is right-angled.
In \[∆ ABC, if a = \sqrt{2}, b = \sqrt{3} \text{ and } c = \sqrt{5}\] show that its area is \[\frac{1}{2}\sqrt{6} sq .\] units.
The sides of a triangle are a = 4, b = 6 and c = 8. Show that \[8 \cos A + 16 \cos B + 4 \cos C = 17\]
In ∆ABC, prove the following:
\[2 \left( bc \cos A + ca \cos B + ab \cos C \right) = a^2 + b^2 + c^2\]
In ∆ABC, prove the following:
\[\left( c^2 - a^2 + b^2 \right) \tan A = \left( a^2 - b^2 + c^2 \right) \tan B = \left( b^2 - c^2 + a^2 \right) \tan C\]
a cos A + b cos B + c cos C = 2b sin A sin C
In ∆ABC, prove the following:
\[a^2 = \left( b + c \right)^2 - 4 bc \cos^2 \frac{A}{2}\]
In ∆ABC, prove the following:
\[4\left( bc \cos^2 \frac{A}{2} + ca \cos^2 \frac{B}{2} + ab \cos^2 \frac{C}{2} \right) = \left( a + b + c \right)^2\]
In \[∆ ABC, \frac{b + c}{12} = \frac{c + a}{13} = \frac{a + b}{15}\] Prove that \[\frac{\cos A}{2} = \frac{\cos B}{7} = \frac{\cos C}{11}\]
In \[∆ ABC, if \angle B = 60°,\] prove that \[\left( a + b + c \right) \left( a - b + c \right) = 3ca\]
In \[∆ ABC \text{ if } \cos C = \frac{\sin A}{2 \sin B}\] prove that the triangle is isosceles.
Answer the following questions in one word or one sentence or as per exact requirement of the question.In a ∆ABC, if b =\[\sqrt{3}\] and \[\angle A = 30°\] find a.
Answer the following questions in one word or one sentence or as per exact requirement of the question.
In a ∆ABC, if \[\cos A = \frac{\sin B}{2\sin C}\] then show that c = a.
Answer the following questions in one word or one sentence or as per exact requirement of the question.
In a ∆ABC, if b = 20, c = 21 and \[\sin A = \frac{3}{5}\]
Answer the following questions in one word or one sentence or as per exact requirement of the question.
In ∆ABC, if a = 8, b = 10, c = 12 and C = λA, find the value of λ.
Mark the correct alternative in each of the following:
In a ∆ABC, if a = 2, \[\angle B = 60°\] and\[\angle C = 75°\]
Mark the correct alternative in each of the following:
In any ∆ABC, 2(bc cosA + ca cosB + ab cosC) =
Mark the correct alternative in each of the following:
In a ∆ABC, if \[\left( c + a + b \right)\left( a + b - c \right) = ab\] then the measure of angle C is
Mark the correct alternative in each of the following:
In any ∆ABC, the value of \[2ac\sin\left( \frac{A - B + C}{2} \right)\] is
Mark the correct alternative in each of the following:
In any ∆ABC, \[a\left( b\cos C - c\cos B \right) =\]
If x = sec Φ – tan Φ and y = cosec Φ + cot Φ then show that xy + x – y + 1 = 0
[Hint: Find xy + 1 and then show that x – y = –(xy + 1)]
