Advertisements
Advertisements
प्रश्न
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष हैं:
(2, 3), (-1, 0), (2, -4)
उत्तर
माना A(2, 3), B(-1, 0) एवं C(2, -4)
∆ = `1/2` [x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2)]
∆ = `1/2` [2 (0 + 4) + (-1) (-4 - 3) + (2) (3 - 0)]
ar (ABC) = `1/2` [2 (4) + (-1) (-7) + 2 (3)]
= `1/2` [8 + 7 + 6]
= 21
वर्ग मात्रक अतः दिए हुए त्रिभुज का अभीष्ट क्षेत्रफल = `21/2` वर्ग मात्रक है।
APPEARS IN
संबंधित प्रश्न
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष हैं:
(-5, -1), (3, -5), (5, 2)
किसी त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है। उस त्रिभुज ABC के लिए इस परिणाम का सत्यापन कीजिए जिसके शीर्ष A(4, -6), B(3, -2) और C(5, 2) हैं।
कृष्णानगर के एक सेकेंडरी स्कूल के कक्षा X के विद्यार्थियों को उनके बागवानी क्रियाकलाप के लिए, एक आयताकार भूखंड दिया गया है। गुलमोहर की पौध (sapling) को परस्पर 1m की दूरी पर इस भूखंड की परिसीमा (boundary) पर लगाया जाता है। इस भूखंड के अंदर एक त्रिभुजाकार घास लगा हुआ लॉन (lawn) है, जैसाकि आकृति में दर्शाया गया है। विद्यार्थियों को भूखंड के शेष भाग में है फूलों के पौधे के बीज बोने हैं।
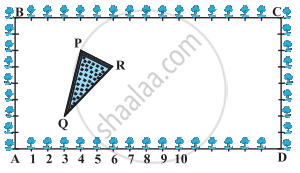
(i) A को मूलबिंदु मानते हए, त्रिभुज के शीषों के निर्देशांक ज्ञात कीजिए।
(ii) यदि मूलबिंदु C हो, तो ∆PQR के शीर्षों के निर्देशांक क्या होंगे?
साथ ही, उपरोक्त दोनों स्थितियों में, त्रिभुजों के क्षेत्रफल ज्ञात कीजिए। आप क्या देखते हैं?
बिंदुओं A(-1, -1), B(-1, 4), C(5, 4) और D(5, -1) से एक आयत ABCD बनता है। P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं। क्या चतुर्भुज PQRS एक वर्ग है? क्या यह एक आयत है? क्या यह एक समचतुर्भुज है? सकारण उत्तर दीजिए।
शीर्षों (a, b + c), (b, c + a) और (c, a + b) वाले त्रिभुज का क्षेत्रफल ______ हैं।
A(6, 1), B(8, 2) और C(9, 4) एक समांतर चतुर्भुज ABCD के तीन शीर्ष हैं। यदि E भुजा DC का मध्य-बिंदु है, तो ΔADE का क्षेत्रफल ज्ञात कीजिए।
एक समबाहु त्रिभुज का परिमाप 60 m है। इसका क्षेत्रफल है
आधार 4 cm और ऊँचाई 6 cm वाले त्रिभुज का क्षेत्रफल 24 cm2 है।
एक त्रिभुज का परिमाप 50 cm है। त्रिभुज की एक भुजा छोटी भुजा से 4 cm लंबी है तथा तीसरी भुजा छोटी भुजा के दुगुने से 6 cm कम है। त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
एक समलंब का क्षेत्रफल 475 cm2 है तथा ऊँचाई 19 cm है। इसकी समांतर भुजाओं की लंबाइयाँ ज्ञात कीजिए, यदि एक समांतर भुजा दूसरी समांतर भुजा से 4 cm अधिक है।
