Advertisements
Advertisements
प्रश्न
Using the property of determinants and without expanding, prove that:
`|(x, a, x+a),(y,b,y+b),(z,c, z+ c)| = 0`
उत्तर
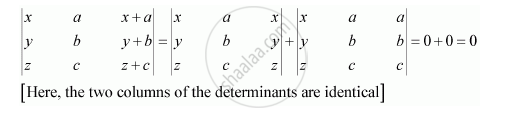
APPEARS IN
संबंधित प्रश्न
Find values of x, if `|[2,3],[4,5]|=|[x,3],[2x,5]|`
Without expanding at any stage, find the value of:
`|(a,b,c),(a+2x,b+2y,c+2z),(x,y,z)|`
A matrix A of order 3 × 3 has determinant 5. What is the value of |3A|?
Let A = [aij] be a square matrix of order 3 × 3 and Cij denote cofactor of aij in A. If |A| = 5, write the value of a31 C31 + a32 C32 a33 C33.
A matrix A of order 3 × 3 is such that |A| = 4. Find the value of |2 A|.
If A is a 3 × 3 invertible matrix, then what will be the value of k if det(A–1) = (det A)k.
Which of the following is not correct?
Which of the following is not correct in a given determinant of A, where A = [aij]3×3.
If A is a matrix of order 3 and |A| = 8, then |adj A| = __________ .
Solve the following system of linear equations using matrix method:
3x + y + z = 1
2x + 2z = 0
5x + y + 2z = 2
Using matrices, solve the following system of linear equations :
x + 2y − 3z = −4
2x + 3y + 2z = 2
3x − 3y − 4z = 11
Without expanding, show that Δ = `|("cosec"^2theta, cot^2theta, 1),(cot^2theta, "cosec"^2theta, -1),(42, 40, 2)|` = 0
Show that Δ = `|(x, "p", "q"),("p", x, "q"),("q", "q", x)| = (x - "p")(x^2 + "p"x - 2"q"^2)`
If Δ = `|(0, "b" - "a", "c" - "a"),("a" - "b", 0, "c" - "b"),("a" - "c", "b" - "c", 0)|`, then show that ∆ is equal to zero.
If x = – 4 is a root of Δ = `|(x, 2, 3),(1, x, 1),(3, 2, x)|` = 0, then find the other two roots.
If x, y ∈ R, then the determinant ∆ = `|(cosx, -sinx, 1),(sinx, cosx, 1),(cos(x + y), -sin(x + y), 0)|` lies in the interval.
The determinant ∆ = `|(sqrt(23) + sqrt(3), sqrt(5), sqrt(5)),(sqrt(15) + sqrt(46), 5, sqrt(10)),(3 + sqrt(115), sqrt(15), 5)|` is equal to ______.
The determinant ∆ = `|(cos(x + y), -sin(x + y), cos2y),(sinx, cosx, siny),(-cosx, sinx, cosy)|` is independent of x only.
If a + b + c ≠ 0 and `|("a", "b","c"),("b", "c", "a"),("c", "a", "b")|` 0, then prove that a = b = c.
Prove tha `|("bc" - "a"^2, "ca" - "b"^2, "ab" - "c"^2),("ca" - "b"^2, "ab" - "c"^2, "bc" - "a"^2),("ab" - "c"^2, "bc" - "a"^2, "ca" - "b"^2)|` is divisible by a + b + c and find the quotient.
If x + y + z = 0, prove that `|(x"a", y"b", z"c"),(y"c", z"a", x"b"),(z"b", x"c", y"a")| = xyz|("a", "b", "c"),("c", "a", "b"),("b", "c", "a")|`
Let f(t) = `|(cos"t","t", 1),(2sin"t", "t", 2"t"),(sin"t", "t", "t")|`, then `lim_("t" - 0) ("f"("t"))/"t"^2` is equal to ______.
If f(x) = `|(0, x - "a", x - "b"),(x + "b", 0, x - "c"),(x + "b", x + "c", 0)|`, then ______.
If A = `[(2, lambda, -3),(0, 2, 5),(1, 1, 3)]`, then A–1 exists if ______.
There are two values of a which makes determinant, ∆ = `|(1, -2, 5),(2, "a", -1),(0, 4, 2"a")|` = 86, then sum of these number is ______.
If A is a matrix of order 3 × 3, then (A2)–1 = ______.
`|(0, xyz, x - z),(y - x, 0, y z),(z - x, z - y, 0)|` = ______.
`"A" = abs ((1/"a", "a"^2, "bc"),(1/"b", "b"^2, "ac"),(1/"c", "c"^2, "ab"))` is equal to ____________.
The value of the determinant `abs ((1,0,0),(2, "cos x", "sin x"),(3, "sin x", "cos x"))` is ____________.
If `Delta = abs((5,3,8),(2,0,1),(1,2,3)),` then write the minor of the element a23.
Let A be a square matrix of order 2 x 2, then `abs("KA")` is equal to ____________.
The value of determinant `|(sin^2 13°, sin^2 77°, tan135°),(sin^2 77°, tan135°, sin^2 13°),(tan135°, sin^2 13°, sin^2 77°)|` is
Value of `|(2, 4),(-1, 2)|` is
