Advertisements
Advertisements
प्रश्न
Without using Pythagoras theorem show that points A(4, 4), B(3, 5) and C(−1, −1) are the vertices of a right angled triangle.
उत्तर
Given, A(4, 4), B(3, 5), C(−1, −1).
Slope of AB = `(y_2 - y_1)/(x_2 - x_1) = (5 - 4)/(3 - 4)` = −1
Slope of BC = `(-1 - 5)/(-1 - 3) = (-6)/(-4) = 3/2`
Slope of AC = `(-1 - 4)/(-1 - 4)` = 1
Slope of AB x slope of AC = −1 × 1 = −1
∴ side AB ⊥ side AC
Thus ΔABC is a right angled triangle right angled at A.
∴ The given points are the vertices of a right angled triangle.
APPEARS IN
संबंधित प्रश्न
Find the slope of the following line which passes through the points:
A(2, −1), B(4, 3)
Find the slope of the following line which passes through the points:
C(−2, 3), D(5, 7)
Find the slope of the following line which passes through the points:
E(2, 3), F(2, −1)
Find the slope of the following line which passes through the points:
G(7, 1), H(−3, 1)
If the X and Y-intercepts of lines L are 2 and 3 respectively then find the slope of line L.
Find the slope of the line whose inclination is 30°
Find the slope of the line which makes angle of 45° with the positive direction of the Y-axis measured anticlockwise
Find the acute angle between the X-axis and the line joining points A(3, −1) and B(4, −2).
A line passes through points A(x1, y1) and B(h, k). If the slope of the line is m then show that k − y1 = m(h − x1)
Select the correct option from the given alternatives:
A line passes through (2, 2) and is perpendicular to the line 3x + y = 3. Its y−interecpt is
Select the correct option from the given alternatives:
The angle between the line `sqrt(3)x - y - 2` = 0 and `x - sqrt(3)y + 1` = 0 is
Select the correct option from the given alternatives:
If kx + 2y − 1 = 0 and 6x − 4y + 2 = 0 are identical lines, then determine k
Answer the following question:
Find the value of k if the slope of the line passing through the points P(3, 4), Q(5, k) is 9
Answer the following question:
Find the value of k the point P(1, k) lies on the line passing through the points A(2, 2) and B(3, 3)
Answer the following question:
Find the equation of the line containing the point T(7, 3) and having inclination 90°.
Answer the following question:
Line through A(h, 3) and B(4, 1) intersect the line 7x − 9y − 19 = 0 at right angle Find the value of h
Find the equation of the lines passing through the point (1, 1) with y-intercept (– 4)
If P(r, c) is midpoint of a line segment between the axes then show that `x/"r" + y/"c"` = 2
The normal boiling point of water is 100°C or 212°F and the freezing point of water is 0°C or 32°F. Find the value of C for 98.6°F
An object was launched from a place P in constant speed to hit a target. At the 15th second, it was 1400 m from the target, and at the 18th second 800 m away. Find time taken to hit the target
Find the equation of the straight lines passing through (8, 3) and having intercepts whose sum is 1
Show that the points (1, 3), (2, 1) and `(1/2, 4)` are collinear, by using any other method
A 150 m long train is moving with constant velocity of 12.5 m/s. Find time taken to cross the bridge of length 850 m
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time is shown in the following table
| Weight (kg) | 2 | 4 | 5 | 8 |
| Length (cm) | 3 | 4 | 4.5 | 6 |
Draw a graph showing the results.
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time is shown in the following table
| Weight (kg) | 2 | 4 | 5 | 8 |
| Length (cm) | 3 | 4 | 4.5 | 6 |
What is the actual length of the spring
A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (Full weight 29.5kg includes the empty cylinders tare weight of 15.3kg.). If it is used with constant rate then it lasts for 24 days. Then the new cylinder is replaced. Find the equation relating the quantity of gas in the cylinder to the days
A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (Full weight 29.5kg includes the empty cylinders tare weight of 15.3kg.). If it is used with constant rate then it lasts for 24 days. Then the new cylinder is replaced. Draw the graph for first 96days
In a shopping mall there is a hall of cuboid shape with dimension 800 × 800 × 720 units, which needs to be added the facility of an escalator in the path as shown by the dotted line in the figure. Find the minimum total length of the escalator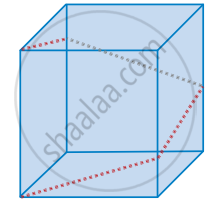
In a shopping mall there is a hall of cuboid shape with dimension 800 × 800 × 720 units, which needs to be added the facility of an escalator in the path as shown by the dotted line in the figure. Find the slopes of the escalator at the turning points
Choose the correct alternative:
Equation of the straight line perpendicular to the line x − y + 5 = 0, through the point of intersection the y-axis and the given line
Choose the correct alternative:
The y-intercept of the straight line passing through (1, 3) and perpendicular to 2x − 3y + 1 = 0 is
A point on the straight line, 3x + 5y = 15 which is equidistant from the coordinate, axes will lie only in ______.
The number of possible tangents which can be drawn to the curve 4x2 – 9y2 = 36, which are perpendicular to the straight line 5x + 2y – 10 = 0 is ______.
The locus of the midpoint of the portion intercept between the axes by the line xcosa + ysina = P where P is a constant is ______.
Find the coordinates of the point which divides the line segment joining the points (1, –2, 3) and (3, 4, –5) internally in the ratio 2 : 3.
