Advertisements
Advertisements
प्रश्न
यदि a < b और c < 0, तो `a/c` ______ `b/c`
उत्तर
यदि a < b और c < 0, तो `a/c` > `b/c`
स्पष्टीकरण:
क्योंकि दोनों पक्षों को समान ऋणात्मक संख्या से गुणा करने पर असमिका का चिह्न बदल जाता है।
APPEARS IN
संबंधित प्रश्न
दी गई असमिका का हल ज्ञात कीजिए तथा संख्या रेखा पर आलेखित कीजिए।
3x - 2 < 2x +1
दी गई असमिका का हल ज्ञात कीजिए तथा संख्या रेखा पर आलेखित कीजिए।
5x – 3 ≥ 3x -5
असमिका 3x – 5 < x + 7 को हल कीजिए जहाँ x एक प्राकृतिक संख्या है।
असमिका 3x – 5 < x + 7 को हल कीजिए जहाँ x एक पूर्ण संख्या है।
असमिका 3x – 5 < x + 7 को हल कीजिए जहाँ x एक पूर्णाक है।
असमिका 3x – 5 < x + 7 को हल कीजिए जहाँ x एक वास्तविक संख्या है।
`(x - 2)/(x + 5) > 2` को हल कीजिए।
किसी उत्पाद के लागत फलन एवं राजस्व फलन क्रमशः C(x) = 20x + 4000 एवं R(x) = 60x + 2000 हैं जहाँ x निर्मित की गईं एवं बेची गईं वस्तुओं की संख्या है। कुछ लाभ अर्जित करने के लिए कितनी वस्तुएँ अवश्य बेची जानी चाहिए?
|x + 1| + |x| > 3 को x के लिए हल कीजिए।
निम्नलिखित असमिका निकाय को हल कीजिए:
`x/(2x + 1) ≥ 1/4, (6x)/(4x - 1) < 1/2`
यदि x ≥ –3, तो x + 5 ______ 2
यदि –x ≤ –4, तो 2x ______ 8
यदि `1/(x - 2) < 0`, तो x ______ 2
यदि p > 0 एवं q < 0, तो p + q ______ p
निम्नलिखित असमिका को x के लिए हल कीजिए:
`(|x - 2| - 1)/(|x - 2| - 2) ≤ 0`
निम्नलिखित असमिका को x के लिए हल कीजिए:
`-5 ≤ (2 - 3x)/4 ≤ 9`
निम्नलिखित असमिका को x के लिए हल कीजिए:
4x + 3 ≥ 2x + 17, 3x – 5 < –2
कैसेट बनाने वाली किसी कंपनी के लागत एवं राजस्व फलन क्रमश: C(x) = 26,000 + 30x एवं R(x) = 43x है, जहाँ x एक सप्ताह में निर्मित किए गए एवं बेचे गए कैसेटों की संख्या है। कुछ लाभ अर्जित करने के लिए कंपनी द्वारा कितनी कैसेट अवश्य बेचे जाने चाहिए?
यदि x < 5, तो
दिया हुआ है कि x, y, b वास्तविक संख्याएँ हैं और x < y, b < 0, तब
यदि −3x + 17 < −13, तो
यदि x वास्तविक संख्या है और |x| < 3, तो
यदि |x + 2| ≤ 9, तो
दिए हुए आलेख को प्रदर्शित करने वाली असमिका निम्नलिखित में से कौन-सी है।
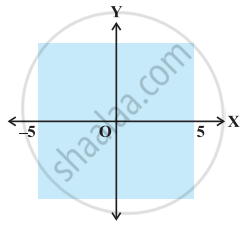
बताइए निम्नलिखित कथन सत्य है या असत्य है?
यदि x < y और b < 0, तो `x/b<y/b`
