Advertisements
Online Mock Tests
Chapters
▶ 2: Relations and Functions
3: Trigonometric Functions
4: Complex Numbers and Quadratic Equations
5: Linear Inequalities
6: Permutations and Combinations
7: Binomial Theorem
8: Sequences and Series
9: Straight Lines
10: Conic Sections
11: Introduction to Three Dimensional Geometry
12: Limits and Derivatives
13: Statistics
14: Probability
![NCERT solutions for Mathematics [English] Class 11 chapter 2 - Relations and Functions NCERT solutions for Mathematics [English] Class 11 chapter 2 - Relations and Functions - Shaalaa.com](/images/mathematics-english-class-11_6:6ab366e2671b448497dd3d3a0e6fed94.jpg)
Advertisements
Solutions for Chapter 2: Relations and Functions
Below listed, you can find solutions for Chapter 2 of CBSE, Karnataka Board PUC NCERT for Mathematics [English] Class 11.
NCERT solutions for Mathematics [English] Class 11 2 Relations and Functions EXERCISE 2.1 [Pages 27 - 28]
If `(x/3+1, y-2/3)` = `(5/3,1/3),`find the values of x and y.
If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in (A × B).
If G = {7, 8} and H = {5, 4, 2}, find G × H and H × G.
State whether the following statement is true or false. If the statement is false, rewrite the given statement correctly.
If P = {m, n} and Q = {n, m}, then P × Q = {(m, n), (n, m)}.
True
False
State whether the following statement is true or false. If the statement is false, rewrite the given statement correctly.
If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that x ∈ A and y ∈ B.
True
False
State whether the following statement is true or false. If the statement is false, rewrite the given statement correctly.
If A = {1, 2}, B = {3, 4}, then A × (B ∩ Φ) = Φ.
True
False
If A = {–1, 1}, find A × A × A.
If A × B = {(a, x), (a, y), (b, x), (b, y)}. Find A and B.
Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that A × (B ∩ C) = (A × B) ∩ (A × C)
Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that A × C is a subset of B × D
Let A = {1, 2} and B = {3, 4}. Write A × B. How many subsets will A × B have? List them.
Let A and B be two sets such that n(A) = 3 and n (B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y and z are distinct elements.
The Cartesian product A × A has 9 elements among which are found (–1, 0) and (0, 1). Find the set A and the remaining elements of A × A.
NCERT solutions for Mathematics [English] Class 11 2 Relations and Functions EXERCISE 2.2 [Pages 29 - 30]
Let A = {1, 2, 3, …, 14}. Define a relation R from A to A by R = {(x, y): 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range.
Define a relation R on the set N of natural numbers by R = {(x, y): y = x + 5, x is a natural number less than 4; x, y ∈ N}. Depict this relationship using roster form. Write down the domain and the range.
A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}. Write R in roster form.
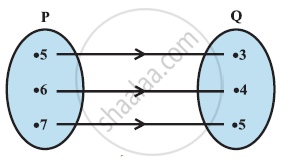
The given figure shows a relationship between the sets P and Q. Write this relation
- in set-builder form.
- in roster form.
What is its domain and range?
Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a, b ∈ A, b is exactly divisible by a}.
- Write R in roster form
- Find the domain of R
- Find the range of R.
Determine the domain and range of the relation R defined by R = {(x, x + 5): x ∈ {0, 1, 2, 3, 4, 5}}.
Write the relation R = {(x, x3): x is a prime number less than 10} in roster form.
Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.
Let R be the relation on Z defined by R = {(a, b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.
NCERT solutions for Mathematics [English] Class 11 2 Relations and Functions EXERCISE 2.3 [Page 38]
Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
- {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
- {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
- {(1, 3), (1, 5), (2, 5)}
Find the domain and range of the given real function:
f(x) = – |x|
Find the domain and range of the following real function:
f(x) = `sqrt(9 - x^2)`
A function f is defined by f(x) = 2x – 5. Write down the values of f(0).
The function ‘t’ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by `t(C) = "9C"/5 + 32`
Find
(i) t(0)
(ii) t(28)
(iii) t(–10)
(iv) The value of C, when t(C) = 212.
Find the range of the following function.
f(x) = 2 – 3x, x ∈ R, x > 0.
Find the range of the following function.
f(x) = x2 + 2, x, is a real number.
Find the range of the following function.
f(x) = x, x is a real number
NCERT solutions for Mathematics [English] Class 11 2 Relations and Functions Miscellaneous Exercise [Pages 40 - 41]
The function f is defined by \[f\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 3 \\ 3x, & 3 \leq x \leq 10\end{cases}\]
The relation g is defined by \[g\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 2 \\ 3x, & 2 \leq x \leq 10\end{cases}\]
Show that f is a function and g is not a function.
If f(x) = x2, find \[\frac{f\left( 1 . 1 \right) - f\left( 1 \right)}{\left( 1 . 1 \right) - 1}\]
Find the domain of the function f(x) = `(x^2 + 2x + 1)/(x^2 - 8x + 12)`
Find the domain and the range of the real function f defined by `f(x)=sqrt((x-1))`
Find the domain and the range of the real function f defined by f (x) = |x – 1|.
Let `f = {(x, x^2/(1+x^2)):x ∈ R}` be a function from R into R. Determine the range of f.
Let f, g: R → R be defined, respectively by f(x) = x + 1, g(x) = 2x – 3. Find f + g, f – g and `f/g`
Let f = {(1, 1), (2, 3), (0, –1), (–1, –3)} be a function from Z to Z defined by f(x) = ax + b, for some integers a, b. Determine a, b.
Let R be a relation from N to N defined by R = {(a, b): a, b ∈ N and a = b2}. Is the following true?
(a, a) ∈ R, for all a ∈ N
Justify your answer in case.
True
False
Let R be a relation from N to N defined by R = {(a, b) : a, b ∈ N and a = b2}. Is the statement true?
(a, b) ∈ R implies (b, a) ∈ R
Justify your answer in case.
True
False
Let R be a relation from N to N defined by R = {(a, b) : a, b ∈ N and a = b2}. Is the statement true?
(a, b) ∈ R and (b, c) ∈ R implies (a, c) ∈ R
Justify your answer in case.
True
False
Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Is the following true?
f is a relation from A to B
Justify your answer in case.
True
False
Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Is the following true?
f is a function from A to B
Justify your answer in case.
True
False
Let f be the subset of Z × Z defined by f = {(ab, a + b): a, b ∈ Z}. Is f a function from Z to Z: justify your answer.
Let A = {9, 10, 11, 12, 13} and let f: A → N be defined by f(n) = the highest prime factor of n. Find the range of f.
Solutions for 2: Relations and Functions
![NCERT solutions for Mathematics [English] Class 11 chapter 2 - Relations and Functions NCERT solutions for Mathematics [English] Class 11 chapter 2 - Relations and Functions - Shaalaa.com](/images/mathematics-english-class-11_6:6ab366e2671b448497dd3d3a0e6fed94.jpg)
NCERT solutions for Mathematics [English] Class 11 chapter 2 - Relations and Functions
Shaalaa.com has the CBSE, Karnataka Board PUC Mathematics Mathematics [English] Class 11 CBSE, Karnataka Board PUC solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT solutions for Mathematics Mathematics [English] Class 11 CBSE, Karnataka Board PUC 2 (Relations and Functions) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 11 chapter 2 Relations and Functions are Cartesian Product of Sets, Brief Review of Cartesian System of Rectanglar Co-ordinates, Concept of Relation, Concept of Functions, Some Functions and Their Graphs, Algebra of Real Functions, Ordered Pairs, Equality of Ordered Pairs, Pictorial Diagrams, Graph of Function, Pictorial Representation of a Function, Exponential Function, Logarithmic Functions, Cartesian Product of Sets, Brief Review of Cartesian System of Rectanglar Co-ordinates, Concept of Relation, Concept of Functions, Some Functions and Their Graphs, Algebra of Real Functions, Ordered Pairs, Equality of Ordered Pairs, Pictorial Diagrams, Graph of Function, Pictorial Representation of a Function, Exponential Function, Logarithmic Functions.
Using NCERT Mathematics [English] Class 11 solutions Relations and Functions exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Solutions are essential questions that can be asked in the final exam. Maximum CBSE, Karnataka Board PUC Mathematics [English] Class 11 students prefer NCERT Textbook Solutions to score more in exams.
Get the free view of Chapter 2, Relations and Functions Mathematics [English] Class 11 additional questions for Mathematics Mathematics [English] Class 11 CBSE, Karnataka Board PUC, and you can use Shaalaa.com to keep it handy for your exam preparation.
