Advertisements
Advertisements
Question
200 लट्ठों (logs) को ढेरी के रूप में इस प्रकार रखा जाता है : सबसे नीचे वाली पंक्ति में 20 लट्ठे, उससे अगली पंक्ति में 19 लट्ठे, उससे अगली पंक्ति में 18 लट्ठे, इत्यादि (देखिए आकृति)। ये 200 लठ्ठे कितनी पंक्तियों में रखे गए हैं तथा सबसे ऊपरी पंक्ति में कितने लट्ठे हैं?
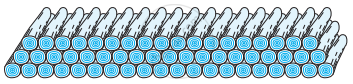
Solution
यह देखा जा सकता है कि पंक्तियों में लट्ठों की संख्या एक A.P. में है।
20, 19, 18…
इस A.P. के लिए,
a = 20
d = a2 − a1
= 19 − 20
= −1
मान लीजिए कि कुल 200 लट्ठों को n पंक्तियों में रखा गया है।
Sn = 200
`S_n = n/2 [2a+(n-1)d]`
`200 = n/2 [2(20)+(n-1)(-1)]`
400 = n (40 − n + 1)
400 = n (41 − n)
400 = 41n − n2
n2 − 41n + 400 = 0
n2 − 16n − 25n + 400 = 0
n (n − 16) − 25 (n − 16) = 0
(n − 16) (n − 25) = 0
या तो (n − 16) = 0 या n− 25 = 0
n = 16 या n = 25
an = a + (n − 1)d
a16 = 20 + (16 − 1) (−1)
a16 = 20 − 15
a16 = 5
इसी प्रकार,
a25 = 20 + (25 − 1) (−1)
a25 = 20 − 24
a25 = −4
स्पष्ट रूप से, 16वीं पंक्ति में लट्ठे की संख्या 5 है। हालाँकि, 25वीं पंक्ति में लट्ठे की संख्या ऋणात्मक है, जो संभव नहीं है।
इसलिए, 16 पंक्तियों में 200 लट्ठे रखे जा सकते हैं और 16वीं पंक्ति में लट्ठे की संख्या 5 है।
APPEARS IN
RELATED QUESTIONS
एक A.P. में, d = 5 और S9 = 75 दिया है। a और a9 ज्ञात कीजिए।
AP: –2, –7, –12,... का कौन-सा पद –77 है? पद –77 तक इस AP का योग ज्ञात कीजिए।
किसी AP में यदि Sn = 3n2 + 5n और ak = 164 है, तो k का मान ज्ञात कीजिए।
उस AP के सभी 11 पदों का योग ज्ञात कीजिए, जिसका मध्य पद 30 है।
AP: −15, −13, −11,... का योग −55 बनाने के लिए इसके कितने पदों की आवश्यकता होगी? दो उत्तर प्राप्त होने का कारण स्पष्ट कीजिए।
प्रथम पद 8 और सार्व अंतर 20 वाली एक AP के प्रथम n पदों का योग एक अन्य AP के प्रथम 2n पदों के योग के बराबर है, जिसका प्रथम पद –30 और सार्व अंतर 8 है। n ज्ञात कीजिए।
यासमीन पहले महीने में 32 रु की बचत करती है, दूसरे महीने में 36 रु की बचत करती है तथा तीसरे महीने में 40 रु की बचत करती है। यदि वह इसी प्रकार बचत करती रहे, तो कितने महीने में वह 2000 रु की बचत कर लेगी?
100 और 200 के बीच के उन पूर्णांकों का योग ज्ञात कीजिए, जो 9 से विभाज्य नहीं हैं।
[संकेत (ii) : ये संख्याएँ होंगी : कुल संख्याएँ– 9 से विभाज्य संख्याएँ]
दर्शाइए कि उस AP का योग, जिसका प्रथम पद a, द्वितीय पद b और अंतिम पद c हो, `((a + c)(b + c - 2a))/(2(b - a))` के बराबर है।
समीकरण – 4 + (−1) + 2 + ... + x = 437 को हल कीजिए।
