Advertisements
Advertisements
Question
36 cm परिमाप वाले आयत की विमाएँ ज्ञात कीजिए जिसे उसकी भुजाओं में से किसी एक के चारों ओर घुमाने पर अधिक से अधिक सम्भव आयतन प्रसर्प (sweep) हो।
Solution
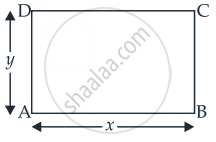
मान लीजिए x और y दिए गए आयत ABCD की लंबाई और चौड़ाई है, प्रश्न के अनुसार, आयत AD के चारों ओर घूमती है जो त्रिज्या x ऊँचाई y वाला एक बेलन बनाएगी।
∴ बेलन का आयतन V = `(pi"r"^2)/"h"`
⇒ V = `pix^2y` .....(i)
अब आयत P का परिमाप = 2(x + y)
⇒ 36 = 2(x + y)
⇒ x + y = 18
⇒ y = 18 – x ....(iii)
y का मान समीकरण (i) में रखना हमें मिलता है
V = `pix^2(18 - x)`
⇒ V = `pi(18x^2 - x^3)`
दोनों पक्षों में अंतर करना w.r.t. x, हमें मिलता है
`"dV"/"dx" = pi(36x - 3x^2)` ....(iii)
`"dV"/"dx"` = 0 स्थानीय उच्चिष्ठ और स्थानीय निम्निष्ठ के लिए,
∴ `pi(36x - 3x^2)` = 0
⇒ 36x – 3x2 = 0
⇒ 3x(12 – x) = 0
⇒ x 0
∴ 12 – x = 0
⇒ x = 12
समीकरण (ii) से
y = 18 – 12 = 6
विभेदक समीकरण (iii) w.r.t. x,
हमें मिलता है `("d"^2"V")/("dx"^2) = pi(36 - 6x)`
x = 12 पर `("d"^2"V")/("dx"^2)`
= `pi(36 - 6 xx 12)`
= `pi(36 - 72)`
= `- 36pi < 0` उच्चिष्ठ
अब इस प्रकार बने बेलन का आयतन = `pix^2y`
= `pi xx (12)^2 xx 6`
= `pi xx 144 xx 6`
= 864π cm3
इसलिए, अभीष्ट आयाम 12 cm और 6 cm और tअधिकतम आयतन 864π cm3 है।
APPEARS IN
RELATED QUESTIONS
सिद्ध कीजिए कि f (x) = `(log x)/x` द्वारा प्रदत्त फलन x = e पर उच्चतम है।
फलन f(x) = `- 3/4 x^4 - 8x^3 - 45/2 x^2 + 105` के सभी स्थानीय उच्चिष्ठ तथा स्थानीय निम्निष्ठ बिंदुओं को ज्ञात कीजिए।
किसी शांकवीय बर्तन के शीर्ष के एक छोटे छिद्र से, जिसका अक्ष ऊर्घ्वाधर है, पानी 1 cu cm/sec की दर से बह रहा है। बर्तन में पानी के सतह की तिर्यक ऊँचाई के घटने की दर उस समय ज्ञात कीजिए जब तिर्यक ऊँचाई 4 cm हैं। शांकवीय बर्तन का शीर्ष कोण `pi/6` है।
वक्र y2 = 4ax तथा x2 = 4by का प्रतिच्छेद कोण ज्ञात कीजिए।
सिद्ध कीजिए कि वक्र x = 3cos θ – cos3θ, y = 3sinθ – sin3θ के किसी बिंदु पर अभिंलब का समीकरण 4 (y cos3θ – x sin3θ) = 3 sin 4θ
वक्र y2 = x पर वह बिंदु जहाँ स्पर्श रेखा x-अक्ष से `pi/4` कोण बनाती है।
a के वे मान जिनके लिए y = x2 + ax + 25 x-अक्ष को स्पर्श करता है, ______ है।
यदि f (x) = `1/(4x^2 + 2x + 1)`, तो इसका उच्चतम मान ______ है।
मान लीजिए कि c पर f का द्वितीय अवकलज है, इस प्रकार कि f ′(c) = 0 तथा f ″(c) > 0, तो c पर फलन ______ है।
नमक का एक गोलाकार गेंद पानी में इस प्रकार घुल रहा है कि किसी क्षण उसके आयतन के घटने की दर उसके पृष्ठीय क्षेत्रफल के समानुपाती है। सिद्ध कीजिए कि उसकी त्रिज्या एक अचर दर से घट रही है।
एक पतंग 151.5 cm की ऊंचाई पर क्षैतिज दिशा में गतिमान है। यदि पतंग की चाल 10 m/s है, तो डोरी को कितनी तेजी से छोड़ा जा रहा है, जब उसकी दूरी पतंग उड़ाने वाले लड़के से 250 cm है? लड़के की ऊंचाई 1.5 m है।
एक दूसरे से 45° पर झुकी हुई दो सड़कों के संधि-स्थल से दो मनुष्य A तथा B, एक ही समय v वेग से चलना प्रारम्भ करते हैं। यदि वे अलग-अलग सड़कों पर चलते हैं तो उनके परस्पर एक दूसरे से अलग होने की दर ज्ञात कीजिए।
(1.999)5 का सन्निकट मान ज्ञात कीजिए।
2m लंबा एक मनुष्य 1`2/3` m/s की दर से किसी बिजली के खंभे की ओर, जो जमीन से 5`1/3`m ऊपर है, चल रहा है। उसकी छाया का अग्रभाग किसी दर से गतिमान है? उसकी छाया की लंबाई, उस समय किस दर से परिवर्तित हो रही है, जब वह प्रकाश के स्रोत के आधार से 3`1/3`m दूर है?
x तथा y दो वर्गों की भुजाएँ हैं, इस प्रकार कि y = x – x2 दूसरे वर्ग के क्षेत्रफल में परिवर्तनकी दर पहले वर्ग के क्षेत्रफल के सापेक्ष ज्ञात कीजिए।
वक्र 2x = y2 तथा 2xy = k के लंबकोणीय प्रतिच्छेद के लिए प्रतिबंध ज्ञात कीजिए।
सिद्ध कीजिए कि वक्र y2 = 4x तथा x2 + y2 – 6x + 1 = 0 एक दूसरे को बिंदु (1, 2) पर स्पर्श करते हैं।
सिद्ध कीजिए कि f (x) = sinx + `sqrt3` cosx का उच्चिष्ठ मान x = `pi/6` पर है।
AB किसी वृत्त का एक व्यास है तथा C उसकी परिधि पर कोई बिंदु है। सिद्ध कीजिए कि ∆ ABC का क्षेत्रफल महत्तम उस समय होगा जब वह समद्धिबाहु है।
यदि वक्र ay + x2 = 7 तथा x3 = y बिंदु (1, 1) पर लंबवत काटते हैं, तो a का मान है ______
वक्र y (1 + x2 ) = 2 – x के, उस बिंदु पर, जहाँ यह x-अक्ष को काटती है, स्पर्श रेखा का समीकरण ______
वक्र x = t2 + 3t – 8, y = 2t2 – 2t – 5 की, बिंदु (2, -1) पर, स्पर्श रेखा की प्रवणता ______ है।
मान लीजिए कि f : R → R, f (x) = 2x + cosx द्वारा परिभाषित है, तो f ______
निम्नलिखित में से कौन-सा फलन 0, `pi/2` में हासमान है,
यदि x एक वास्तविक संख्या है, तो x2 – 8x + 17 का निम्नतम मान ______
वक् y = –x3 + 3x2 + 9x – 27 की उच्चतम प्रवणता ______
`(1/x)^x`का उच्चतम मान है ______
वक्र y = tanx के (0, 0) पर अभिलंब का समीकरण ______ है।
