Advertisements
Advertisements
Question
2m लंबा एक मनुष्य 1`2/3` m/s की दर से किसी बिजली के खंभे की ओर, जो जमीन से 5`1/3`m ऊपर है, चल रहा है। उसकी छाया का अग्रभाग किसी दर से गतिमान है? उसकी छाया की लंबाई, उस समय किस दर से परिवर्तित हो रही है, जब वह प्रकाश के स्रोत के आधार से 3`1/3`m दूर है?
Solution
माना AB बिजली के खंभे की ऊंचाई है और CD आदमी की ऊंचाई इस प्रकार है कि
AB = `5 1/3 = 16/3 "m"` और CD = 2 m
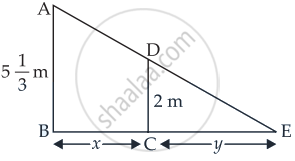
माना BC = x लंबाई (बिजली के खम्भे से आदमी की दूरी) और CE = y किसी भी समय आदमी की छाया की लंबाई है।
आकृति से, हम देखते हैं कि
ΔABE ~ Δ DCE ......[AAA समानता द्वारा]
∴ उनकी संगत भुजाओं का अनुपात लेते हुए, हम प्राप्त करते हैं
`"AB"/"CD" = "BE"/"CE"`
⇒ `"AB"/"CD" = ("BC" + "CE")/"CE"`
⇒ `(16/3)/2 = (x + y)/y`
⇒ `8/3 = (x + y)/y`
⇒ 8y = 3x + 3y
⇒ 8y – 3y = 3x
⇒ 5y = 3x
दोनों पक्षों को w.r.t, t, से अलग करने पर, हम प्राप्त करते हैं
`"dy"/"dt" = 3 * "dx"/dt"`
⇒ `"dy"/"dt" = 3/5 * "dx"/"dt"`
⇒ `"dy"/"dt" = 3/5 * ((-5)/3)` ......[∵ आदमी विपरीत दिशा में चल रहा है]
= – 1 m/s
अतः छाया की लंबाई 1 m/s की दर से घट रही है।
अब मान लीजिए u = x + y .....(u = प्रकाश स्तंभ से छाया के सिरे की दूरी)
दोनों पक्षों में अंतर करना w.r.t. t, हमें मिलता है
`"du"/"dt" = "dx"/"dt" + "dy"/dt"`
= `(- 1 2/3 - 1)`
= `-(5/3 + 1)`
= `- 8/3`
= `-2 2/3` m/s
अतः छाया का सिरा `2 2/3` m/s की दर से प्रकाश स्तंभ की ओर गति कर रहा है तथा छाया की लंबाई 1 m/s की दर से घट रही है।
APPEARS IN
RELATED QUESTIONS
वक्र y = 5x – 2x3 के लिए, यदि x में 2 इकाई/से. की दर से वृद्धि हो रही है, तो x = 3 पर वक्र का प्रावण्य कितनी तीव्रता से परिवर्तित हो रहा है?
वक्र y2 = x तथा x2 = y के बीच का प्रतिच्छेद - कोण ज्ञात कीजिए।
सिद्ध कीजिए कि फलन f(x) = 4x3 – 18x2 + 27x – 7 का कोई उच्चिष्ठ अथवा निम्निष्ठ नहीं है।
अवकलों के प्रयोग द्वारा `sqrt(0.082)` का सन्निकट मान ज्ञात कीजिए।
शीर्ष कोण `2theta` वाला एक समद्धिबाहु त्रिभुज a त्रिज्या वाले किसी वृत्त के अंतर्गत स्थित है। सिद्ध कीजिए कि त्रिभुजं का क्षेत्रफल उच्चतम है। जब `theta = pi/6`
दो वक्र x3 – 3xy2 + 2 = 0 तथा 3x2 y – y3 = 2
समीकरण x = et . cost, y = et . sint द्वारा प्रदत्त वक्र की t = `pi/4` पर स्पर्श रेखा, x-अक्ष से कोण बनाती है।
किसी गोले के आयतन के परिवर्तन की दर उसके पृष्ठीय क्षेत्रफल के सापेक्ष, जब उसकी त्रिज्या 2cm है, ______ है।
नमक का एक गोलाकार गेंद पानी में इस प्रकार घुल रहा है कि किसी क्षण उसके आयतन के घटने की दर उसके पृष्ठीय क्षेत्रफल के समानुपाती है। सिद्ध कीजिए कि उसकी त्रिज्या एक अचर दर से घट रही है।
यदि किसी वृत्त का क्षेत्रफल एक समान दर से बढ़ता है, तो सिद्ध कीजिए कि उसका परिमाप (परिधि) उसकी त्रिज्या के व्युत्क्रमानुपाती होता है
एक खोखले बेलनाकार खोल, जिसकी आंतरिक तथा बाह्य त्रिज्याएँ क्रमश: 3 cm तथा 3.0005 cm हैं, में धातु के आयतन का सन्निकट मान ज्ञात कीजिए।
वक्र 2x = y2 तथा 2xy = k के लंबकोणीय प्रतिच्छेद के लिए प्रतिबंध ज्ञात कीजिए।
सिद्ध कीजिए कि वक्र xy = 4 तथा x2 + y2 = 8, एक दूसरे को स्पर्श करते हैं।
वक्र y = 4 – x2 तथा y = x2 का प्रतिच्छेद-कोण ज्ञात कीजिए।
वक्र x2 + y2 – 2x – 4y + 1 = 0 के किन बिंदुओं पर स्पर्श रेखाएँ y-अक्ष के समांतर हैं।
सिद्ध कीजिए कि a ≥ 1 के लिए f (x) = `sqrt3` sinx - cosx - 2ax + b, R में हासमान फलन है।
यदि किसी समकोण त्रिभुज की एक भुजा तथा कर्ण की लंबाईयों का योगफल दिया हुआ है, तो सिद्ध कीजिए कि त्रिभुज का क्षेत्रफल उच्चतम है, जब उनके मध्य का कोण `pi/3` है।
वर्गाकार आधार तथा ऊर्ध्वाधर पृष्ठ वाले धातु के किसी बाक्स में 1024 cm3 वस्तु आती है। शीर्ष तथा आधार के पृष्ठों के माल (वस्तु) का मूल्य Rs 5/cm2 है तथा पृष्ठों के मान का मूल्य Rs 2.50/cm2 हैं। बाक्स का निम्नतम मूल्य ज्ञात कीजिए।
यदि y = x4 – 10 तथा यदि x, 2 से 1.99 तक परिवर्तित होता है, तो y का परिवर्तन क्या (कितना) है,
वक्र y (1 + x2 ) = 2 – x के, उस बिंदु पर, जहाँ यह x-अक्ष को काटती है, स्पर्श रेखा का समीकरण ______
फलन f(x) = 4 sin3x – 6 sin2x + 12 sinx + 100 ______
निम्नलिखित में से कौन-सा फलन 0, `pi/2` में हासमान है,
यदि x एक वास्तविक संख्या है, तो x2 – 8x + 17 का निम्नतम मान ______
sin x . cos x का उच्चतम मान है ______
f (x) = 2 sin3x + 3 cos3x का मान x = `(5pi)/6`, पर ______
f(x) = xx का स्तब्ध बिंदु है ______
a के वे मान जिनके लिए फलन f (x) = sinx – ax + b, R में वर्धमान है ______ .हैं।
