Advertisements
Advertisements
Question
4 सेमी, 5 सेमी और 6 सेमी भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर उसके समरूप एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ पहले त्रिभुज की संगत भुजाओं की `2/3` हों। निर्माण का औचित्य बताइए।
Solution
चरण 1
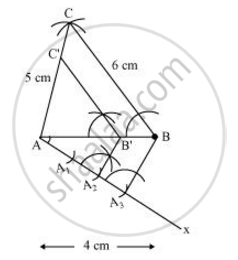
एक रेखाखंड AB = 4 सेमी खींचिए। बिंदु A को केंद्र मानकर 5 सेमी त्रिज्या का एक चाप खींचिए। इसी प्रकार, बिंदु B को केंद्र मानकर 6 सेमी त्रिज्या का एक चाप खींचिए। ये चाप एक दूसरे को बिंदु C पर काटेंगे। अब, AC = 5 सेमी और BC = 6 सेमी और ΔABC अभीष्ट त्रिभुज है।
चरण 2
शीर्ष C के विपरीत दिशा में रेखा AB के साथ न्यून कोण बनाते हुए एक किरण AX खींचिए।
चरण 3
लाइन AX पर 3 बिंदु A1, A2, A3 (जैसा कि 2 और 3 के बीच बड़ा है) का पता लगाएँ जैसे कि AA1 = A1A2 = A2A3
चरण 4
BA3 को मिलाइए और A2 से होकर BA3 के समानांतर एक रेखा खींचिए जो AB को बिंदु B पर काटती है।
चरण 5
रेखा BC के समांतर B' से होकर एक रेखा खींचिए जो AC को C' पर प्रतिच्छेद करे।
ΔABC' अभीष्ट त्रिभुज है।
औचित्य
निर्माण को सिद्ध करके उचित ठहराया जा सकता है कि
`AB' = 2/3AB, B'C' = 2/3BC, AC' = 2/3 AC`
निर्माण से, हमारे पास B'C' || BC पूर्व
∴ ∠AB'C'= ∠ABC (सभी तरीके से)
In ΔAB'C' and ΔABC,
∠AB'C' = ∠ABC (ऊपर सिद्ध)
∠B'AC' = ∠BAC (ऊपर सिद्ध)
∴ ΔAB'C' ~ ΔABC (AA समानता मानदंड)
`=> (AB')/(AB) = (B'C')/(BC) = (AC')/(AC) ....(1)`
In ΔAA2B' and ΔAA3B,
∠A2AB' = ∠A3AB (सामान्य)
∠AA2B' = ∠AA3B (सभी तरीके से)
∴ ΔAA2B' ∼ ΔAA3B (AA समानता मानदंड)
`=> (AB')/(AB) = (`
`=> (AB')/(AB) = 2/3 ....(2)`
समीकरण (1) और (2) से, हम प्राप्त करते हैं
`(AB')/(AB) = (B'C')/(BC) = (AC')/(AC) = 2/3`
`=>AB' = 2/3(AB), B'C' = 2/3(BC), AC' = 2/3(AC)`
यह निर्माण को सही ठहराता है।
APPEARS IN
RELATED QUESTIONS
आधार 8 सेमी और ऊँचाई 4 सेमी एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजा समद्विबाहु त्रिभुज की संगत भुजाओं की `1 1/2` गुणा है।निर्माण का औचित्य बताइए
एक त्रिभुज ABC बनाइए जिसमें BC = 6 सेमी, AB = 5 सेमी और ∠ABC = 60 हो। फिर एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ ΔABC की संगत भुजाओं की `3/4` गुनी हों। औचित्य बताइए
एक त्रिभुज ABC बनाइए, जिसमें BC = 7 सेमी, ∠B = 45°, ∠A = 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की `4/3` गुनी हों। और औचित्य बताइए
एक दिये हुए त्रिभुज ABC के समरूप एक ऐसा त्रिभुज बनाने के लिए जिसकी भुजाएँ ΔABC की संगत भुजाओं का `8/5` हों, पहले एक किरण BX ऐसी खींचिए कि ∠CBX एक न्यून कोण हो और X भुजा BC के सापेक्ष A के विपरीत ओर हो। किरण BX पर अब समान दूरियों पर अंकित किये जाने वाले बिंदुओं की न्यूनतम संख्या है।
एक दिये हुए त्रिभुज के समरूप एक ऐसे त्रिभुज की रचना करने के लिए जिसकी भुजाएँ ΔABC की संगत भुजाओं का `7/3` हों, BC से एक न्यून कोण बनाती हुई एक किरण BX खींचिए, ताकि X भुजा BC के सापेक्ष A के विपरीत ओर स्थित हो। BX पर समान दूरियों पर बिंदु B1, B2, ...., B7, अंकित कीजिए, B3 को C से मिलाइए और फिर B3C के समांतर एक रेखाखंड B6C' खींचा जाता है, जबकि बिंदु C' बढ़ाई गयी भुजा BC पर स्थित है। अंत में, AC के समांतर रेखाखंड A'C' खींचा जाता है।
एक समकोण त्रिभुज ABC खींचिए, जिसमें BC = 12 cm, AB = 5 cm और ∠B = 90° है। इस त्रिभुज के समरूप एक त्रिभुज की रचना कीजिए, जिसका स्केल गुणक `2/3` हो। क्या नया त्रिभुज भी एक समकोण त्रिभुज है?
एक त्रिभुज ABC खींचिए, जिसमें BC = 6 cm, CA = 5 cm और AB = 4 cm है। इस त्रिभुज के समरूप और स्केल गुणक `5/3` के एक त्रिभुज की रचना कीजिए।
दो रेखाखंडों AB और AC के बीच का कोण 60° है, जहाँ AB = 5 cm और AC = 7 cm है। AB और AC पर क्रमश : बिंदु P और Q इस प्रकार निर्धारित कीजिए कि AP = `3/4` AB और AQ = `1/4` AC हो। P और Q को मिलाइए तथा PQ की लंबाई ज्ञात कीजिए।
एक समांतर चतुर्भुज ABCD खींचिए, जिसमें BC = 5 cm, AB = 3 cm और ∠ABC = 60° है। विकर्ण BD द्वारा इसे दो त्रिभुजों BCD और ABD में विभाजित कीजिए।
एक त्रिभुज ABC खींचिए, जिसमें AB = 4 cm, BC = 6 cm और AC = 9 cm है। इस ΔABC के समरूप, स्केल गुणक `3/2` के एक त्रिभुज की रचना कीजिए। रचना का औचित्य दीजिए क्या दोनों त्रिभुज सर्वांगसम हैं? ध्यान दीजिए कि यहाँ दोनों त्रिभुजों में तीनों कोण और दो भुजाएँ बराबर हैं।
