Advertisements
Advertisements
Question
एक त्रिभुज ABC खींचिए, जिसमें BC = 6 cm, CA = 5 cm और AB = 4 cm है। इस त्रिभुज के समरूप और स्केल गुणक `5/3` के एक त्रिभुज की रचना कीजिए।
Solution
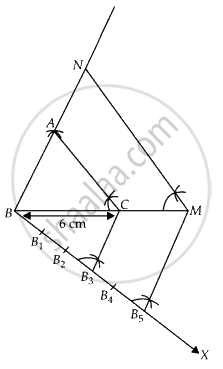
निर्माण के चरण:
- एक रेखाखंड BC = 6 cm खींचिए।
- B और C को केंद्र मानकर 4 cm और 5 cm त्रिज्या के दो चाप खींचिए जो एक दूसरे को A पर काटते हैं।
- BA और CA ज्वाइन करें। ∆ABC अभीष्ट त्रिभुज है।
- B से, न्यूनकोण बनाते हुए कोई भी किरण BX नीचे की ओर खींचिए।
- BX पर पांच बिंदु B1, B2, B3, B4 और B5 अंकित करें, जैसे कि BB1 = B1B2 = B2B3 = B3B4 = B4B5।
- B3C से जुड़ें और B5 से ड्रा करें B5M || B3C विस्तारित रेखा खंड BC को M पर प्रतिच्छेद करता है।
- बिंदु M से खींचिए MN || CA विस्तारित रेखा खंड BA को N पर प्रतिच्छेद करता है।
फिर, ∆NBM आवश्यक त्रिभुज है जिसकी भुजाएँ ∆ABC की संगत भुजाओं के `5/3` के बराबर हैं।
अतः, ∆NBM अभीष्ट त्रिभुज है।
APPEARS IN
RELATED QUESTIONS
4 सेमी, 5 सेमी और 6 सेमी भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर उसके समरूप एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ पहले त्रिभुज की संगत भुजाओं की `2/3` हों। निर्माण का औचित्य बताइए।
5 सेमी, 6 सेमी और 7 सेमी भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ पहले त्रिभुज की संगत भुजाओं की `7/5` हों। निर्माण का औचित्य बताइए।
एक त्रिभुज ABC बनाइए, जिसमें BC = 7 सेमी, ∠B = 45°, ∠A = 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की `4/3` गुनी हों। और औचित्य बताइए
एक समकोण त्रिभुज बनाइए, जिसकी भुजाएँ (कर्ण के अलावा) 4 सेमी और 3 सेमी लंबी हों। एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए गए त्रिभुज की संगत भुजाओं की `5/3` गुनी हों। निर्माण का औचित्य बताइए।
एक रेखाखंड AB को 5 : 7 के अनुपात में विभाजित करने के लिए, पहले एक किरण AX खींचिए, ताकि ∠BAX एक न्यून कोण हो और फिर किरण AX पर समान दूरियों पर बिंदु अंकित किये जाएँ ताकि इनकी न्यूनतम संख्या हो ______।
एक दिये हुए त्रिभुज ABC के समरूप एक ऐसा त्रिभुज बनाने के लिए जिसकी भुजाएँ ΔABC की संगत भुजाओं का `3/7` हों, पहले एक किरण BX ऐसी खींचिए कि ∠CBX एक न्यून कोण हो और X भुजा BC के सापेक्ष A के विपरीत ओर हो। किरण BX पर अब समान दूरियों पर बिंदु B1, B2, B3, ... अंकित कीजिए तथा उसके बाद अगला चरण मिलाने का है ______।
एक दिये हुए त्रिभुज ABC के समरूप एक ऐसा त्रिभुज बनाने के लिए जिसकी भुजाएँ ΔABC की संगत भुजाओं का `8/5` हों, पहले एक किरण BX ऐसी खींचिए कि ∠CBX एक न्यून कोण हो और X भुजा BC के सापेक्ष A के विपरीत ओर हो। किरण BX पर अब समान दूरियों पर अंकित किये जाने वाले बिंदुओं की न्यूनतम संख्या है।
दो रेखाखंडों AB और AC के बीच का कोण 60° है, जहाँ AB = 5 cm और AC = 7 cm है। AB और AC पर क्रमश : बिंदु P और Q इस प्रकार निर्धारित कीजिए कि AP = `3/4` AB और AQ = `1/4` AC हो। P और Q को मिलाइए तथा PQ की लंबाई ज्ञात कीजिए।
एक समद्विबाहु त्रिभुज ABC खींचिए, जिसमें AB = AC = 6 cm और BC = 5 cm है। ΔABC के समरूप, एक त्रिभुज PQR की रचना कीजिए, जिसमें PQ = 8 cm हो।अपनी रचना का औचित्य भी दीजिए।
एक त्रिभुज ABC खींचिए, जिसमें AB = 4 cm, BC = 6 cm और AC = 9 cm है। इस ΔABC के समरूप, स्केल गुणक `3/2` के एक त्रिभुज की रचना कीजिए। रचना का औचित्य दीजिए क्या दोनों त्रिभुज सर्वांगसम हैं? ध्यान दीजिए कि यहाँ दोनों त्रिभुजों में तीनों कोण और दो भुजाएँ बराबर हैं।
