Advertisements
Advertisements
Question
A converging lens of focal length 12 cm and a diverging mirror of focal length 7.5 cm are placed 5.0 cm apart with their principal axes coinciding. Where should an object be placed so that its image falls on itself?
Solution
Let the object be placed at a distance x cm from the lens (away from the mirror).
For the convex lens (1st refraction) u = − x, f = − 12 cm
From the lens formula:
\[\frac{1}{v} - \frac{1}{u} = \frac{1}{f}\Rightarrow\frac{1}{v}=\frac{1}{( - 12)}+\frac{1}{( - x)}\Rightarrow v=-\left( \frac{12x}{x + 12} \right)\]
Thus, the virtual image due to the first refraction lies on the same side as that of object A'B'.
This image becomes the object for the convex mirror,
For the mirror,
\[u = - \left( 5 + \frac{12x}{x + 12} \right)\]
\[ = - \left( \frac{17x + 60}{x + 12} \right)\]
\[f = - 7 . 5 \text{ cm }\]
From mirror equation,
\[\frac{1}{v} + \frac{1}{u} = \frac{1}{f}\]
\[ \Rightarrow \frac{1}{v} = \frac{1}{- 7 . 5} + \frac{x + 12}{17x + 60}\]
\[ \Rightarrow \frac{1}{v} = \frac{17x + 60 - 7 . 5}{7 . 5(17x + 60)}\]
\[\Rightarrow v = \frac{7 . 5(17x + 60)}{52 . 5 - 127 . 5x}\]
\[ \Rightarrow v = \frac{250(x + 4)}{15x - 100}\]
\[ \Rightarrow v = \frac{50(x + 4)}{(3x - 20)}\]
Thus, this image is formed towards the left of the mirror.
Again for second refraction in concave lens,
\[u = - \left[ \frac{5 - 50(x + 4)}{3x - 20} \right]\]
(assuming that the image of mirror formed between the lens and mirror is 3x − 20),
v = + x (since, the final image is produced on the object A"B")
Using lens formula:
\[\frac{1}{v} - \frac{1}{u} = \frac{1}{f}\]
\[ \Rightarrow \frac{1}{x}+\frac{1}{\frac{\left[ 5 - 50 (x \times 4) \right]}{3x - 20}}=\frac{1}{- 20}\]
⇒ 25x2 − 1400x − 6000 = 0
⇒ x2 − 56x − 240 = 0
⇒ (x − 60) (x + 4) = 0
Thus, x = 60 m
The object should be placed at a distance 60 cm from the lens farther away from the mirror, so that the final image is formed on itself.
APPEARS IN
RELATED QUESTIONS
A small candle, 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?
A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of the image and the magnification. Describe what happens as the needle is moved farther from the mirror.
In motor vehicles, a convex mirror is attached near the driver's seat to give him the view of the traffic behind. What is the special function of this convex mirror which a plane mirror can not do?
Can mirrors give rise to chromatic aberration?
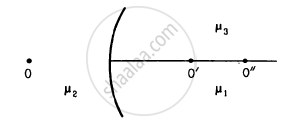
Following figure shows three transparent media of refractive indices \[\mu_1 , \mu_2 \text{ and } \mu_3\]. A point object O is placed in the medium \[\mu_2\]. If the entire medium on the right of the spherical surface has refractive index \[\mu_3\], the image forms at O". In the situation shown,
A man uses a concave mirror for shaving. He keeps his face at a distance of 25 cm from the mirror and gets an image which is 1.4 times enlarged. Find the focal length of the mirror.
The image of an extended object, placed perpendicular to the principal axis of a mirror, will be erect if
(a) the object and the image are both real
(b) the object and the image are both virtual
(c) the object is real but the image is virtual
(d) the object is virtual but the image is real.
A spherical surface of radius 30 cm separates two transparent media A and B with refractive indices 1.33 and 1.48 respectively. The medium A is on the convex side of the surface. Where should a point object be placed in medium A so that the paraxial rays become parallel after refraction at the surface?
How can the spherical aberration produced by a lens be minimized?
According to Cartesian sign convention, all distances are measured from the _______.
A thin converging lens of focal length 12 cm is kept in contact with a thin diverging lens of focal length 18 cm. Calculate the effective/equivalent focal length of the combination.
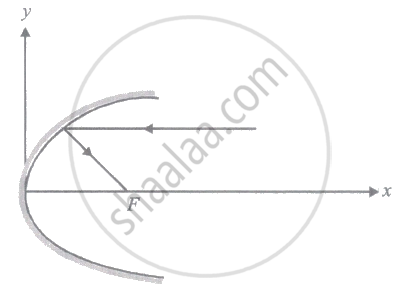
A parallel beam of light ray parallel to the x-axis is incident on a parabolic reflecting surface x = 2by2 as shown in the figure. After reflecting it passes through focal point F. What is the focal length of the reflecting surface?
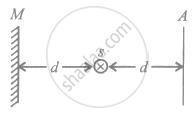
The intensity of a point source of light, S, placed at a distance d in front of a screen A, is I0 at the center of the screen. Find the light intensity at the center of the screen if a completely reflecting plane mirror M is placed at a distance d behind the source, as shown in the figure.
A car is moving with at a constant speed of 60 km h–1 on a straight road. Looking at the rear view mirror, the driver finds that the car following him is at a distance of 100 m and is approaching with a speed of 5 km h–1. In order to keep track of the car in the rear, the driver begins to glance alternatively at the rear and side mirror of his car after every 2 s till the other car overtakes. If the two cars were maintaining their speeds, which of the following statement (s) is/are correct?
Parallel rays striking a spherical mirror far from the optic axis are focussed at a different point than are rays near the axis thereby the focus moves toward the mirror as the parallel rays move toward the outer edge of the mirror. What value of incidence angle θ produces a 2% change in the location of the focus, compared to the location for θ very close to zero?
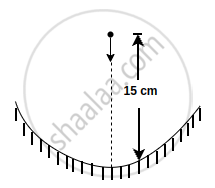
A particle is dropped along the axis from a height 15 cm on a concave mirror of focal length 30 cm as shown in figure. The acceleration due to gravity is 10 m/s2. Find the maximum speed of image in m/s:
A converging lens has a focal length of 10 cm in air. It is made of a material with a refractive index of 1.6. If it is immersed in a liquid of refractive index 1.3, find its new focal length.
