Advertisements
Advertisements
Question
A path of 8 m width runs around the outsider of a circular park whose radius is 17 m. Find the area of the path.
Solution
The radius (r) of the inner circle is 17 m.
The radius (R) of the outer circle is 25 m. [Includes path, i.e (17 + 8)]
Area of the path `= pi"R"^2 - pi"r"^2`
`=pi("R"^2-"r"^2)`
`=22/7(25^2 - 17^2)`
`=22/7xx(25-17)(25+17)`
`=22/7xx8xx42`
= 1056 m2
∴ Area of the path = 1056 m2
APPEARS IN
RELATED QUESTIONS
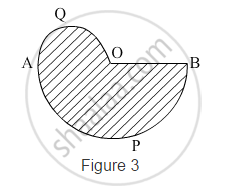
In Fig. 3, APB and AQO are semicircles, and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region [Use `pi=22/7`]
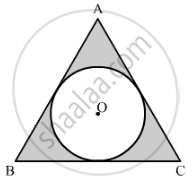
In Fig 4, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.[Use π=3.14 and √3=1.73]
From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)

An arc of length 15 cm subtends an angle of 45° at the centre of a circle. Find in terms of 𝜋, radius of the circle.
The outer circumference of a circular race track is 528m. The track is everywhere 14m
wide. Calculate the cost of leveling the track at rate of 50 paise per square metre.
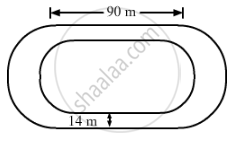
The inside perimeter of a running track shown in the figure is 400 m. The length of each of the straight portions is 90 m, and the ends are semicircles. If the track is 14 m wide everywhere, find the area of the track. Also, find the length of the outer boundary of the track.
Find the area and perimeter of the following semi-circle :
Diameter= 7 cm
Two circles touch each other externally. The sum of their areas is 5811 cm2 and the distance between their centres is 10 cm. Find the radii of the two circles.
Find the diameter of the sphere for the following :
Surface Area = 221. 76 cm2
Circumference of a circle of diameter 5 cm is ______.
