Advertisements
Advertisements
Question
A person observes the angle of elevation of the peak of a hill from a station to be α. He walks c metres along a slope inclined at an angle β and finds the angle of elevation of the peak of the hill to be ϒ. Show that the height of the peak above the ground is \[\frac{c \sin \alpha \sin \left( \gamma - \beta \right)}{\left( \sin \gamma - \alpha \right)}\]
Solution
Suppose, AB is a peak whose height above the ground is t+x.
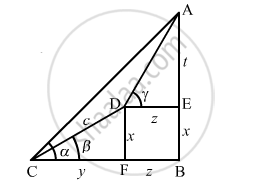
\[In \bigtriangleup DFC, \]
\[\sin\beta = \frac{x}{c} \]
\[ \Rightarrow x = c\sin\beta\]
\[and \]
\[\tan\beta = \frac{x}{y}\]
\[ \Rightarrow y = \frac{x}{\tan\beta} = \frac{c\sin\beta}{\sin\beta} \times \cos\beta = c\cos\beta . . . \left( 1 \right)\]
\[In ∆ ADE, \]
\[\tan\gamma = \frac{t}{z}\]
\[ \Rightarrow z = t \cot\gamma . . . \left( 2 \right)\]
\[\]
\[In ∆ ABC, \]
\[\tan\alpha = \frac{t + x}{y + z}\]
\[\]
\[ \Rightarrow t + x = \left( c\cos\beta\tan\alpha + tcot\gamma \right)\tan\alpha \left( from \left( 1 \right) and \left( 2 \right) \right)\]
\[ \Rightarrow t - tcot\gamma\tan\alpha = c\cos\beta\tan\alpha - c\sin\beta \left( \because x = c\sin\beta \right)\]
\[ \Rightarrow t\left( 1 - \frac{\sin\alpha\cos\gamma}{\cos\alpha\sin\gamma} \right) = c\left( \frac{\cos\beta\sin\alpha - \cos\alpha\sin\beta}{\cos\alpha} \right)\]
\[ \Rightarrow t\left( \frac{\sin\gamma\cos\alpha - \sin\alpha\cos\gamma}{\cos\alpha\sin\gamma} \right) = c\frac{\sin\left( \alpha - \beta \right)}{\cos\alpha}\]
\[ \Rightarrow t\frac{\sin\left( \gamma - \beta \right)}{\cos\alpha\sin\gamma} = c\frac{\sin\left( \alpha - \beta \right)}{\cos\alpha}\]
\[ \Rightarrow t = c\frac{\sin\gamma\sin\left( \alpha - \beta \right)}{\sin\left( \gamma - \beta \right)} . . . \left( 3 \right)\]
\[\text{ Now }, \]
\[AB = t + x = c\frac{\sin\gamma\sin\left( \alpha - \beta \right)}{\sin\left( \gamma - \beta \right)} + c\sin\beta \left( \text{ using }\left( 3 \right) \right)\]
\[ = c\left( \frac{\sin\gamma\sin\left( \alpha - \beta \right)}{\sin\left( \gamma - \beta \right)} + \sin\beta \right)\]
\[ = c\left[ \frac{\sin\gamma\sin\left( \alpha - \beta \right) + \sin\beta\sin\left( \gamma - \beta \right)}{\sin\left( \gamma - \beta \right)} \right]\]
\[ = c\left[ \frac{\sin\gamma\sin\alpha\cos\beta - \sin\beta\sin\gamma\cos\alpha + \sin\beta\sin\gamma\cos\alpha - \sin\beta\cos\gamma\sin\alpha}{\sin\left( \gamma - \beta \right)} \right]\]
\[ = c\left[ \frac{\sin\gamma\sin\alpha\cos\beta - \sin\beta\cos\gamma\sin\alpha}{\sin\left( \gamma - \beta \right)} \right]\]
\[ = c\left[ \frac{\sin\alpha\sin\left( \gamma - \beta \right)}{\sin\left( \gamma - \beta \right)} \right]\]
\[ = \frac{c\sin\alpha\sin\left( \gamma - \beta \right)}{\sin\left( \gamma - \beta \right)}\]
\[\text{ Hence proved } . \]
APPEARS IN
RELATED QUESTIONS
If in ∆ABC, ∠C = 105°, ∠B = 45° and a = 2, then find b.
In ∆ABC, if a = 18, b = 24 and c = 30 and ∠c = 90°, find sin A, sin B and sin C.
In triangle ABC, prove the following:
In triangle ABC, prove the following:
In any triangle ABC, prove the following:
In triangle ABC, prove the following:
\[\frac{a^2 - c^2}{b^2} = \frac{\sin \left( A - C \right)}{\sin \left( A + C \right)}\]
In triangle ABC, prove the following:
In triangle ABC, prove the following:
In triangle ABC, prove the following:
In triangle ABC, prove the following:
In ∆ABC, prove that: \[a \sin\frac{A}{2} \sin \left( \frac{B - C}{2} \right) + b \sin \frac{B}{2} \sin \left( \frac{C - A}{2} \right) + c \sin \frac{C}{2} \sin \left( \frac{A - B}{2} \right) = 0\]
In ∆ABC, prove that \[a \left( \cos C - \cos B \right) = 2 \left( b - c \right) \cos^2 \frac{A}{2} .\]
At the foot of a mountain, the elevation of it summit is 45°; after ascending 1000 m towards the mountain up a slope of 30° inclination, the elevation is found to be 60°. Find the height of the mountain.
In \[∆ ABC, if a = 5, b = 6 a\text{ and } C = 60°\] show that its area is \[\frac{15\sqrt{3}}{2} sq\].units.
In \[∆ ABC, if a = \sqrt{2}, b = \sqrt{3} \text{ and } c = \sqrt{5}\] show that its area is \[\frac{1}{2}\sqrt{6} sq .\] units.
In ∆ ABC, if a = 18, b = 24 and c = 30, find cos A, cos B and cos C.
In ∆ABC, prove the following: \[b \left( c \cos A - a \cos C \right) = c^2 - a^2\]
In ∆ABC, prove the following: \[c \left( a \cos B - b \cos A \right) = a^2 - b^2\]
In ∆ABC, prove the following:
\[\left( c^2 - a^2 + b^2 \right) \tan A = \left( a^2 - b^2 + c^2 \right) \tan B = \left( b^2 - c^2 + a^2 \right) \tan C\]
In ∆ABC, prove the following:
\[\frac{c - b \cos A}{b - c \cos A} = \frac{\cos B}{\cos C}\]
In ∆ABC, prove that \[a \left( \cos B + \cos C - 1 \right) + b \left( \cos C + \cos A - 1 \right) + c\left( \cos A + \cos B - 1 \right) = 0\]
In ∆ABC, prove the following:
\[a^2 = \left( b + c \right)^2 - 4 bc \cos^2 \frac{A}{2}\]
In ∆ABC, prove the following:
\[4\left( bc \cos^2 \frac{A}{2} + ca \cos^2 \frac{B}{2} + ab \cos^2 \frac{C}{2} \right) = \left( a + b + c \right)^2\]
In \[∆ ABC, if \angle B = 60°,\] prove that \[\left( a + b + c \right) \left( a - b + c \right) = 3ca\]
If in \[∆ ABC, \cos^2 A + \cos^2 B + \cos^2 C = 1\] prove that the triangle is right-angled.
Two ships leave a port at the same time. One goes 24 km/hr in the direction N 38° E and other travels 32 km/hr in the direction S 52° E. Find the distance between the ships at the end of 3 hrs.
Answer the following questions in one word or one sentence or as per exact requirement of the question.In a ∆ABC, if b =\[\sqrt{3}\] and \[\angle A = 30°\] find a.
Answer the following questions in one word or one sentence or as per exact requirement of the question.
In ∆ABC, if a = 8, b = 10, c = 12 and C = λA, find the value of λ.
Answer the following questions in one word or one sentence or as per exact requirement of the question.
In any triangle ABC, find the value of \[a\sin\left( B - C \right) + b\sin\left( C - A \right) + c\sin\left( A - B \right)\
Mark the correct alternative in each of the following:
In any ∆ABC, \[\sum^{}_{} a^2 \left( \sin B - \sin C \right)\] =
Mark the correct alternative in each of the following:
In a ∆ABC, if a = 2, \[\angle B = 60°\] and\[\angle C = 75°\]
Mark the correct alternative in each of the following:
In any ∆ABC, 2(bc cosA + ca cosB + ab cosC) =
Mark the correct alternative in each of the following:
In any ∆ABC, the value of \[2ac\sin\left( \frac{A - B + C}{2} \right)\] is
Mark the correct alternative in each of the following:
In any ∆ABC, \[a\left( b\cos C - c\cos B \right) =\]
Find the value of `(1 + cos pi/8)(1 + cos (3pi)/8)(1 + cos (5pi)/8)(1 + cos (7pi)/8)`
