Advertisements
Advertisements
Question
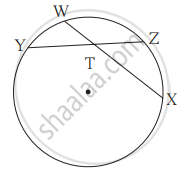
आकृति में, m(चाप WY) = 44°, m(चाप ZX) = 68°, तो
(1) ∠ZTX का माप ज्ञात कीजिए।
(2) WT = 4.8, TX = 8.0, YT = 6.4 तो TZ = कितना?
(3) WX = 25, YT = 8, YZ = 26, तो WT = कितना?
Solution
(1) m(चाप WY) = 44°, m(चाप ZX) = 68° ...........(दिया है |)
∠ZTX का शीर्ष बिंदु, वृत्त के अंतः भाग में है और इस कोण द्वारा चाप ZX अंतःखंडित होता है और इस कोण के विपरीत कोण ∠WTY के द्वारा चाप WY अंतःखंडित होता है |
∴ ∠ZTX = `1/2 xx `[m(चाप WY) + m(चाप ZX)]
∴ ∠ZTX = `1/2 xx [44^circ + 68^circ]`
∴ ∠ZTX = `1/2 xx 112^circ`
∴ ∠ZTX = 56°.
(2) WT = 4.8, TX = 8, YT = 6.4 ...........(दिया है |)
जीवा WX तथा जीवा YZ परस्पर वृत्त के अंतःभाग में प्रतिच्छेदित करते है |
∴ जीवाओं के अंतः छेदन प्रमेय से,
WT × TX = YT × TZ
∴ `4.8 xx 8 = 6.4 xx "TZ"`
∴ TZ = `(4.8 xx 8)/6.4`
∴ TZ = `(4.8 xx 8 xx 10)/(6.4 xx 10)`
∴ TZ = `(48 xx 8)/64`
∴ TZ = 6.
(3) WX = 25, YT = 8, YZ = 26 .......(दिया है |)
YT + TZ = YZ ...........(Y-T-Z)
∴ 8 + TZ = 26
∴ TZ = 26 - 8
∴ TZ = 18
मानो कि, WT = x
WT + TX = WX ...........(W-T-X)
∴ x + TX = 25
∴ TX = (25 - x)
जीवा WX और जीवा YZ परस्पर वृत्त के अंतः भाग में प्रतिच्छेदित करते है |
∴ जीवाओं के अंतः छेदन के प्रमेय से,
WT × TX = YT × TZ
∴ x × (25 - x) = 8 × 18
∴ 25x - x2 = 144
∴ x2 - 25x + 144 = 0
∴ x2 - 16x - 9x + 144 = 0
∴ x(x - 16) - 9(x - 16) = 0
∴ (x - 16)(x - 9) = 0
x - 16 = 0 या x - 9 = 0
∴ x = 16 या x = 9
∴ WT = 16 या WT = 9.
(1) ∠ZTX = 56°.
(2) TZ = 6
(3) WT = 16 या WT = 9.
APPEARS IN
RELATED QUESTIONS
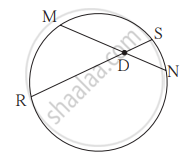
आकृति में, जीवा MN और RS एक दूसरे को बिंदु D पर प्रतिच्छेदित करते हैं।
(1) यदि RD = 15, DS = 4, MD = 8 तो DN = कितना?
(2) यदि RS = 18, MD = 9, DN = 8 तो DS = कितना?
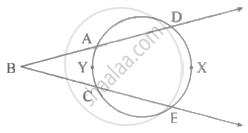
दी गई आकृति में, m(चाप DXE) = 105°, m(चाप AYC) = 47° हो, तो ∠DBE का मान ज्ञात करो।
वृत्त को जीवाएँ AB तथा CD वृत्त के अंत:भाग में बिदु E पर प्रतिच्छेदित करती हैं। यदि AE = 4, EB = 10, CE = 8, तो ED का मान ज्ञात कीजिए?
3 सेमी त्रिज्या वाले वृत्त की सबसे बड़ी जीवा लंबाई = ?
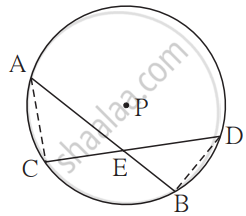
दत्त: वृत्त का केंद्र P है। जीवा AB और जीवा CD परस्पर बिंदु E पर प्रतिच्छेदित करती हैं।
साध्य: AE × EB = CE × ED
रचना: रेख AC और रेख DB खींचिए।
खाली जगह भरकर उपपत्ति पूर्ण कीजिए।
उपपत्ति: ΔCAE और ΔBDE में,
∠AEC ≅ ∠DEB ......... `square`
`square` ≅ ∠BDE .....(एक ही चाप में अंतर्लिखित कोण)
∴ ΔCAE ~ ΔBDE ........ `square`
∴ `square/ ("DE") = ("CE")/square` ........ `square`
∴ AE × EB = CE × ED
