Advertisements
Advertisements
Question
ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.
Solution
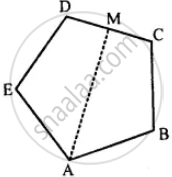
Given: ABCDE is a regular pentagon.
The bisector ∠A of the pentagon meets the side CD at point M.
To prove : ∠AMC = 90°
Proof: We know that the measure of each interior angle of a regular pentagon is 108°.
∠BAM = x 108° = 54°
Since, we know that the sum of a quadrilateral is 360°
In quadrilateral ABCM, we have
∠BAM + ∠ABC + ∠BCM + ∠AMC = 360°
54° + 108° + 108° + ∠AMC = 360°
∠AMC = 360° – 270°
∠AMC = 90°
APPEARS IN
RELATED QUESTIONS
How many diagonals does following have?
A regular hexagon
In a quadrilateral, define of the following Adjacent angles .
Two angles of a quadrilateral are of measure 65° and the other two angles are equal. What is the measure of each of these two angles?
Two angles of a quadrilateral are 68° and 76°. If the other two angles are in the ratio 5 : 7; find the measure of each of them.
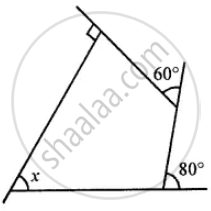
Use the following figure to find the value of x
If three angles of a quadrilateral are 90° each, show that the given quadrilateral is a rectangle.
Three angles of a quadrilateral are 75º, 90º and 75º. The fourth angle is ______.
A pair of opposite sides of a trapezium are ______.
Using the information given, name the right angles in part of figure:
RT ⊥ ST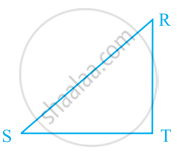
Draw a rough sketch of a quadrilateral KLMN. State two pairs of opposite angles.
