Advertisements
Advertisements
Question
An incomplete distribution is given below:
| Variable: | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Frequency: | 12 | 30 | - | 65 | - | 25 | 18 |
You are given that the median value is 46 and the total number of items is 230.
(i) Using the median formula fill up missing frequencies.
(ii) Calculate the AM of the completed distribution.
Solution
(i)
| Class interval | Frequency | Cumulative frequency |
| 10-20 | 12 | 12 |
| 20-30 | 30 | 42 |
| 30-40 | x | 42 + x |
| 40-50 | 65 | 107 + x |
| 50-60 | y | 107 + x + y |
| 60-70 | 25 | 132 + x + y |
| 70-80 | 18 | 150 + x + y |
| N = 230 |
Given median = 46
Then, median class = 40 - 50
l = 40, h = 50 - 40 = 10, f = 65, F = 42 + x
Median `=l+((N/2)-F)/fxxh`
`rArr46=40+(115-(42+x))/65xx10`
`rArr46 - 40 = (115-42-x)/65xx10`
`rArr6=(73-x)/65=10`
`rArr(6xx65)/10=73-x`
`rArr390/10=73-x`
39 = 73 - x
x = 73 - 39
x = 34
Given N = 230
⇒ 12 + 30 + x + 65 + y + 25 + 18 = 230
⇒ 12 + 30 + 34 + 65 + y + 25 + 18 = 230
⇒ 184 + y = 230
⇒ y = 230 - 184
⇒ y = 46
(ii)
| Class interval | Mid value(x) | Frequency(f) | fx |
| 10-20 | 15 | 12 | 180 |
| 20-30 | 25 | 30 | 750 |
| 30-40 | 35 | 34 | 1190 |
| 40-50 | 45 | 65 | 2925 |
| 50-60 | 55 | 46 | 2530 |
| 60-70 | 65 | 25 | 1625 |
| 70-80 | 75 | 18 | 1350 |
| N = 230 | `sumfx=10550` |
Mean `=(sumfx)/N`
`=10550/230=45.87`
APPEARS IN
RELATED QUESTIONS
Below is the given frequency distribution of words in an essay
| Number of Words | Number of Candidates |
| 600 – 800 | 8 |
| 800 – 1000 | 22 |
| 1000 – 1200 | 40 |
| 1200 – 1400 | 18 |
| 1400 - 1600 | 12 |
Find the mean number of words written.
The numbers 6, 8, 10, 12, 13 and x are arranged in an ascending order. If the mean of the observations is equal to the median, find the value of x
The median of the following observations
11, 12, 14, (x - 2), (x + 4), (x + 9), 32, 38, 47 arranged in ascending order is 24.
Find the value of x and hence find the mean.
An incomplete distribution is given as follows:
| Variable: | 0 - 10 | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 |
| Frequency: | 10 | 20 | ? | 40 | ? | 25 | 15 |
You are given that the median value is 35 and the sum of all the frequencies is 170. Using the median formula, fill up the missing frequencies.
The weight of 60 boys are given in the following distribution table:
| Weight (kg) | 37 | 38 | 39 | 40 | 41 |
| No. of boys | 10 | 14 | 18 | 12 | 6 |
Find:
- Median
- Lower quartile
- Upper quartile
- Inter-quartile range
What is the value of the median of the data using the graph in the following figure of less than ogive and more than ogive?
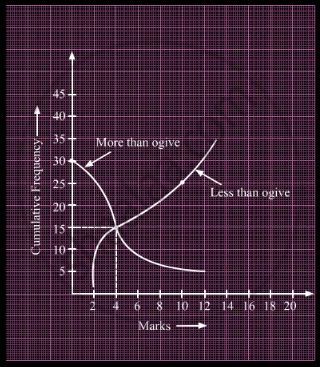
Weekly income of 600 families is tabulated below:
| Weekly income (in Rs) |
Number of families |
| 0 – 1000 | 250 |
| 1000 – 2000 | 190 |
| 2000 – 3000 | 100 |
| 3000 – 4000 | 40 |
| 4000 – 5000 | 15 |
| 5000 – 6000 | 5 |
| Total | 600 |
Compute the median income.
Find the median of the following distribution:
| Marks | 0 – 10 | 10 –20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 |
| Number of students | 5 | 8 | 20 | 15 | 7 | 5 |
If in a frequency distribution, the mean and median are 21 and 22 respectively, then its mode is approximately ______.
A survey conducted on 20 households in a locality by a group of students resulted in the following frequency table for the number of family members in a household:
| Family size | 1 – 3 | 3 – 5 | 5 – 7 | 7 – 9 | 9 – 11 |
| Numbers of Families | 7 | 8 | 2 | 2 | 1 |
Find the median of this data.
