Advertisements
Advertisements
Question
Answer the following :
Find the length of the tangent segment drawn from the point (5, 3) to the circle x2 + y2 + 10x – 6y – 17 = 0
Solution 1
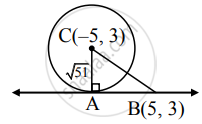
Given equation of circle is
x2 + y2 + 10x – 6y – 17 = 0
Comparing this equation with
x2 + y2 + 2gx + 2fy + c = 0, we get
2g = 10, 2f = –6, c = –17
∴ g = 5, f = –3, c = –17
Centre of circle = (– g, – f )
= C(– 5, 3)
Radius of circle = `sqrt("g"^2 + "f"^2 - "c")`
= `sqrt(5^2 + (-3)^2 - (-17))`
= `sqrt(25 + 9 + 17)`
= `sqrt(51)`
BC = `sqrt((-5 - 5)^2 + (3 - 3)^2`
= `sqrt(100 + 0)`
= 10
In right angled ΔABC
BC2 = AB2 + AC2 …[Pythagoras theorem]
∴ (10)2 = `"AB"^2 + (sqrt(51))^2`
∴ AB2 = 100 – 51 = 49
∴ AB = 7
∴ Length of the tangent segment from (5, 3) is 7 units.
Solution 2
Given equation of circle is
x2 + y2 + 10x – 6y – 17 = 0
Here, g = 5, f = –3, c = –17
Length of the tangent segment to the circle
x2 + y2 + 2gx + 2fy + c = 0 from the point
(x1, y1) is `sqrt(x_1^2 + y_1^2 + 2"g"x_1 + 2"f"y_1 + "c")`.
∴ Length of the tangent segment from (5, 3)
= `sqrt((5)^2 + (3)^2 + 10(5) - 6(3) - 17)`
= `sqrt(25 + 9 + 50 - 18 - 17)`
= `sqrt(49)`
= 7 units
APPEARS IN
RELATED QUESTIONS
Find the equation of the circle with centre at origin and radius 4.
Find the equation of the circle with centre at (−3, −2) and radius 6.
Find the equation of the circle with centre at (−3, −3) passing through the point (−3, −6)
Find the centre and radius of the circle:
x2 + y2 = 25
Find the centre and radius of the circle:
(x − 5)2 + (y − 3)2 = 20
Find the centre and radius of the circle:
`(x - 1/2)^2 + (y + 1/3)^2 = 1/36`
Find the equation of the circle with centre at (a, b) touching the Y-axis
Find the equation of the circle with centre at (–2, 3) touching the X-axis.
Find the equation of the circle with centre on the X-axis and passing through the origin having radius 4.
Find the equation of the circle with centre at (3,1) and touching the line 8x − 15y + 25 = 0
Find the equation circle if the equations of two diameters are 2x + y = 6 and 3x + 2y = 4. When radius of circle is 9
Find the equation of a circle with radius 4 units and touching both the co-ordinate axes having centre in third quadrant.
Find the equation of circle (a) passing through the origin and having intercepts 4 and −5 on the co-ordinate axes
Show that the equation 3x2 + 3y2 + 12x + 18y − 11 = 0 represents a circle
Find the equation of the circle passing through the points (5, 7), (6, 6) and (2, −2)
Show that the points (3, −2), (1, 0), (−1, −2) and (1, −4) are concyclic
Choose the correct alternative:
Equation of a circle which passes through (3, 6) and touches the axes is
Choose the correct alternative:
Find the equation of the circle which passes through the points (2, 3) and (4, 5) and the centre lies on the straight line y − 4x + 3 = 0
Choose the correct alternative:
If a circle passes through the point (0, 0), (a, 0) and (0, b) then find the co-ordinates of its centre
Choose the correct alternative:
The equation of a circle with origin as centre and passing through the vertices of an equilateral triangle whose median is of length 3a is
Answer the following :
Find the centre and radius of the circle x2 + y2 − x +2y − 3 = 0
Answer the following :
Find the equation of circle which passes through the origin and cuts of chords of length 4 and 6 on the positive side of x-axis and y-axis respectively
The line 2x − y + 6 = 0 meets the circle x2 + y2 + 10x + 9 = 0 at A and B. Find the equation of circle on AB as diameter.
Answer the following :
Show that the circles touch each other externally. Find their point of contact and the equation of their common tangent:
x2 + y2 – 4x + 10y +20 = 0,
x2 + y2 + 8x – 6y – 24 = 0.
Answer the following :
Show that the circles touch each other externally. Find their point of contact and the equation of their common tangent:
x2 + y2 – 4x – 10y + 19 = 0,
x2 + y2 + 2x + 8y – 23 = 0.
If 2x - 4y = 9 and 6x - 12y + 7 = 0 are the tangents of same circle, then its radius will be ______
If the radius of a circle increases from 3 cm to 3.2 cm, then the increase in the area of the circle is ______
The equation of circle whose diameter is the line joining the points (–5, 3) and (13, –3) is ______.
Let AB be a chord of the circle x2 + y2 = r2 subtending a right angle at the centre, then the locus of the centroid of the ΔPAB as P moves on the circle is ______.
