Advertisements
Advertisements
Question
Answer the following question.
State Gauss's law for magnetism. Explain its significance.
Solution
The net magnetic flux (ΦB) through any closed surface is always zero.
This law suggests that the number of magnetic field lines leaving any closed surface is always equal to the number of magnetic field lines entering it.

Suppose a closed surface S is held in a uniform magnetic field `vecB`.
Consider a small vector area element Δ`vec"S"` of this surface.
Magnetic flux through this area element is defined as ΔΦB = `vec"B".Δvec"S" `
Considering all small area elements of the surface, we obtain net magnetic flux through the surface as:
ØB = `sum_"All" ΔØ_"B" = sum_"All" vec"B". Δvec"S" = 0`
APPEARS IN
RELATED QUESTIONS
State and explain Gauss’s law.
A charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaces of the cube.
State Gauss’s law for magnetism. Explain its significance.
Answer the following question.
State Gauss's law on electrostatics and drive expression for the electric field due to a long straight thin uniformly charged wire (linear charge density λ) at a point lying at a distance r from the wire.
The Electric flux through the surface
 (i) |
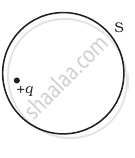 (ii) |
 (iii) |
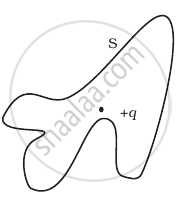 (iv) |
If `oint_s` E.dS = 0 over a surface, then ______.
- the electric field inside the surface and on it is zero.
- the electric field inside the surface is necessarily uniform.
- the number of flux lines entering the surface must be equal to the number of flux lines leaving it.
- all charges must necessarily be outside the surface.
Refer to the arrangement of charges in figure and a Gaussian surface of radius R with Q at the centre. Then
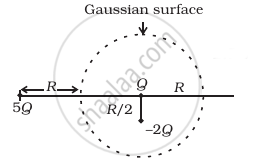
- total flux through the surface of the sphere is `(-Q)/ε_0`.
- field on the surface of the sphere is `(-Q)/(4 piε_0 R^2)`.
- flux through the surface of sphere due to 5Q is zero.
- field on the surface of sphere due to –2Q is same everywhere.
If the total charge enclosed by a surface is zero, does it imply that the elecric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.
In finding the electric field using Gauss law the formula `|vec"E"| = "q"_"enc"/(epsilon_0|"A"|)` is applicable. In the formula ε0 is permittivity of free space, A is the area of Gaussian surface and qenc is charge enclosed by the Gaussian surface. This equation can be used in which of the following situation?
