Advertisements
Advertisements
Question
Answer the following question:
The vertices of a triangle are A(1, 4), B(2, 3) and C(1, 6) Find equations of altitudes of ∆ABC
Solution
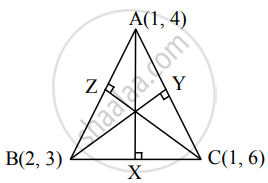
Let AX, BY and CZ be the altitudes through the vertices A, B and C respectively of ∆ABC.
Slope of BC = – 3
∴ Slope of AX = `1/3` ...[∵ AX ⊥ BC]
Since altitude AX passes through (1, 4) and has slope `1/3`,
equation of altitude AX is
y – 4 = `1/3(x - 1)`
∴ 3y – 12 = x – 1
∴ x – 3y + 11 = 0
Since both the points A and C have same x co-ordinates i.e. 1,
the points A and C lie on the line x = 1.
AC is parallel to Y-axis and therefore, altitude
BY is parallel to X-axis
Since the altitude BY passes through B(2, 3),
the equation of altitude BY is y = 3.
Also, slope of AB = – 1
∴ Slope of CZ = 1
Since altitude CZ passes through (1, 6) and has slope 1,
equation of altitude CZ is
y – 6 = 1(x – 1)
∴ x – y + 5 = 0
APPEARS IN
RELATED QUESTIONS
Write the equation of the line :
parallel to the X−axis and at a distance of 5 unit form it and above it
Write the equation of the line :
parallel to the Y−axis and at a distance of 5 unit form it and to the left of it
Write the equation of the line :
parallel to the X-axis and at a distance of 4 unit form the point (−2, 3)
Obtain the equation of the line :
parallel to the X−axis and making an intercept of 3 unit on the Y−axis
Obtain the equation of the line containing the point :
A(2, – 3) and parallel to the Y−axis
Obtain the equation of the line containing the point :
B(4, –3) and parallel to the X-axis
Find the equation of the line passing through the points A(2, 0), and B(3, 4)
Find the equation of the line containing the origin and having inclination 60°
Find the equation of the line having inclination 135° and making X-intercept 7
The vertices of a triangle are A(3, 4), B(2, 0), and C(−1, 6). Find the equation of the line containing side BC.
The vertices of a triangle are A(3, 4), B(2, 0), and C(−1, 6). Find the equation of the line containing the median AD
The vertices of a triangle are A(3, 4), B(2, 0), and C(−1, 6). Find the equation of the line containing the midpoints of sides AB and BC
Find the x and y intercept of the following line:
`x/3 + y/2` = 1
Find the x and y intercept of the following line:
`(3x)/2 + (2y)/3` = 1
Find equations of lines containing the point A(3, 4) and making equal intercepts on the co-ordinates axes.
Select the correct option from the given alternatives:
The equation of the line through (1, 2), which makes equal intercepts on the axes, is
Select the correct option from the given alternatives:
If the line kx + 4y = 6 passes through the point of intersection of the two lines 2x + 3y = 4 and 3x + 4y = 5, then k =
Answer the following question:
Reduce the equation 6x + 3y + 8 = 0 into slope-intercept form. Hence find its slope
Answer the following question:
Does point A(2, 3) lie on the line 3x + 2y – 6 = 0? Give reason.
Answer the following question:
Find the equation of the line having slope 5 and containing point A(–1, 2).
Answer the following question:
Find the equation of the line which contains the point A(3, 5) and makes equal intercepts on the co-ordinates axes.
Answer the following question:
The vertices of a triangle are A(1, 4), B(2, 3) and C(1, 6). Find equations of the sides.
Answer the following question:
Find the equation of the line through A(−2, 3) and perpendicular to the line through S(1, 2) and T(2, 5)
Answer the following question:
Find the Y-intercept of the line whose slope is 4 and which has X intercept 5
Answer the following question:
Find the equations of the diagonals of the rectangle whose sides are contained in the lines x = 8, x = 10, y = 11 and y = 12
Answer the following question:
The vertices of ∆PQR are P(2, 1), Q(−2, 3) and R(4, 5). Find the equation of the median through R.
Answer the following question:
P(a, b) is the mid point of a line segment between axes. Show that the equation of the line is `x/"a" + y/"b"` = 2
If (a, −2a), a > 0 is the mid-point of a line segment intercepted between the co-ordinate axes, then the equation of the line is ____________.
The slope of normal to the curve x = `sqrt"t"` and y = `"t" - 1/sqrt"t"`at t = 4 is _____.
A Plane cuts the coordinate axes X, Y, Z at A, B, C respectively such that the centroid of the Δ ABC is (6, 6, 3). Then the equation of that plane is ______.
Suppose the line `(x - 2)/α = ("y" - 2)/(-5) = ("z" + 2)/2` lies on the plane x + 3y – 2z + β = 0. Then (α + β) is equal to ______.
Let the perpendiculars from any point on the line 7x + 56y = 0 upon 3x + 4y = 0 and 5x – 12y = 0 be p and p', then ______.
N(3, – 4) is the foot of the perpendicular drawn from the origin to a line L. Then, the equation of the line L is ______.
