Advertisements
Advertisements
Questions
Use Gauss' law to derive the expression for the electric field `(vecE)` due to a straight uniformly charged infinite line of charge density λ C/m.
Use Gauss' law to obtain an expression for the electric field due to an infinitely long thin straight wire with uniform linear charge density λ.
Solution
Field due to an infinitely long straight uniformly charged wire,

Consider a thin, infinitely long straight line charge of linear charge density λ.
Let P be the point at a distance a from the line. To find the electric field at point P, draw a cylindrical surface of radius ‘a’ and length l.
If E is the magnitude of the electric field at point P, then electric flux through the Gaussian surface,
Φ = E × Area of the curved surface of a cylinder of radius r and length l
As electric lines of force are parallel to the end faces (circular caps) of the cylinder, there is no component of the field along the normal to the end faces.
Φ = E × 2πal …(i)
According to Gauss's Theorem,
`phi = q/epsilon_0`
`∵ q = lambdal`
`:. phi = (lambdal)/epsilon_0` ...(ii)
From equations (i) and (ii), we get:
`E xx 2pial = (lambdal)/epsilon_0`
APPEARS IN
RELATED QUESTIONS
A 36 cm long sonometer wire vibrates with frequency of 280 Hz in fundamental mode, when it is under tension of 24.5 N. Calculate linear density of the material of wire.
Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss’s law. [Hint: Use Coulomb’s law directly and evaluate the necessary integral.]
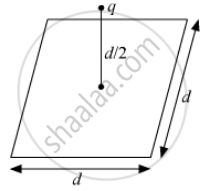
A point charge q is at a distance of d/2 directly above the centre of a square of side d, as shown the figure. Use Gauss' law to obtain the expression for the electric flux through the square.
Find the work done in bringing a charge q from perpendicular distance r1 to r2 (r2 > r1)
A closed surface in vacuum encloses charges –q and +3q. The total electric flux emerging out of the surface is :
The electric field inside a spherical shell of uniform surface charge density is ______.
- Obtain the expression for the electric field intensity due to a uniformly charged spherical shell of radius R at a point distant r from the centre of the shell outside it.
- Draw a graph showing the variation of electric field intensity E with r, for r > R and r < R.
A solid metal sphere of radius R having charge q is enclosed inside the concentric spherical shell of inner radius a and outer radius b as shown in the figure. The approximate variation of the electric field `vecE` as a function of distance r from centre O is given by ______.

Draw a graph of kinetic energy as a function of linear charge density λ.
