Advertisements
Advertisements
Question
अपवर्तनांक 1.55 के काँच से दोनों फलकों की समान वक्रता त्रिज्या के उभयोत्तल लेंस निर्मित करने हैं। यदि 20 cm फोकस दूरी के लेंस निर्मित करने हैं तो अपेक्षित वक्रता त्रिज्या क्या होगी?
Solution
काँच का अपवर्तनांक, μ = 1.55
द्वि-उत्तल लेंस की फोकस दूरी, f = 20 cm
लेंस के एक फलक की वक्रता त्रिज्या = R1
लेंस के दूसरे फलक की वक्रता त्रिज्या = R2
द्वि-उत्तल लेंस की वक्रता त्रिज्या = R
∴ R1 = R and R2 = −R
R का मान इस प्रकार से गणना किया जा सकता है:
`1/"f" = (μ - 1)[1/"R"_1 - 1/"R"_2]`
`1/20 = (1.55 - 1)[1/"R" + 1/"R"]`
`1/20 = 0.55 xx 2/"R"`
R = 0.55 × 2 × 20
∴ R = 22 cm
अतः, द्वि-उत्तल लेंस की वक्रता त्रिज्या 22 cm होगी।
APPEARS IN
RELATED QUESTIONS
कोई टैंक 12.5 cm ऊँचाई तक जल से भरा है। किसी सूक्ष्मदर्शी द्वारा बीकर की तली पर पड़ी किसी सुई की आभासी गहराई 9.4 cm मापी जाती है। जल का अपवर्तनांक क्या है? बीकर में उसी ऊँचाई तक जल के स्थान पर किसी 1.63 अपवर्तनांक के अन्य द्रव से प्रतिस्थापन करने पर सुई को पुनः फोकसित करने के लिए सूक्ष्मदर्शी को कितना ऊपर/नीचे ले जाना होगा?
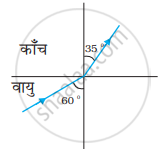
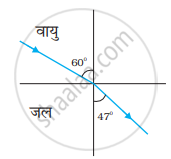
चित्र (a) तथा (b) में किसी आपतित किरण का अपवर्तन दर्शाया गया है जो वायु में क्रमशः काँच-वायु तथा जल-वायु अंतरापृष्ठ के अभिलंब से 60° का कोण बनाती है। उस आपतित किरण का अपवर्तन कोण ज्ञात कीजिए, जो जल में जल-काँच अंतरापृष्ठ के अभिलंब से 45° का कोण बनाती है [चित्र (c)]।
 |
 |
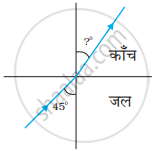 |
| (a) | (b) | (c) |
जल से भरे 80 cm गहराई के किसी टैंक की तली पर कोई छोटा बल्ब रखा गया है। जल के पृष्ठ का वह क्षेत्र ज्ञात कीजिए जिससे बल्ब का प्रकाश निर्गत हो सकता है। जल का अपवर्तनांक 1.33 है। (बल्ब को बिंदु प्रकाश स्रोत मानिए।)
कोई प्रिज्म अज्ञात अपवर्तनांक के काँच का बना है। कोई समांतर प्रकाश-पुंज इस प्रिज्म के किसी फलक पर आपतित होता है। प्रिज्म का न्यूनतम विचलन कोण 40° मापा गया। प्रिज्म के पदार्थ का अपवर्तनांक क्या है? प्रिज्म का अपवर्तन कोण 60° है। यदि प्रिज्म को जल (अपवर्तनांक 1.33) में रख दिया जाए तो प्रकाश के समांतर पुंज के लिए नए न्यूनतम विचलन कोण का परिकलन कीजिए।
किसी मेज के ऊपरी पृष्ठ पर जड़ी एक छोटी पिन को 50 cm ऊँचाई से देखा जाता है। 15 cm मोटे आयताकार काँच के गुटके को मेज के पृष्ठ के समांतर पिन व नेत्र के बीच रखकर उसी बिंदु से देखने पर पिन नेत्र से कितनी दूर दिखाई देगी? काँच की अपवर्तनांक 1.5 है। क्या उत्तर गुटके की अवस्थिति पर निर्भर करता है?
कोई कार्ड शीट जिसे 1 mm2 साइज़ के वर्गों में विभाजित किया गया है, को 9 cm दूरी पर रखकर किसी आवर्धक लेंस (9 cm फोकस दूरी का अभिसारी लेंस) द्वारा उसे नेत्र के निकट रखकर देखा जाता है।
- लेंस द्वारा उत्पन्न आवर्धन (प्रतिबिंब-साइज़/वस्तु-साइज़) क्या है? आभासी प्रतिबिंब में प्रत्येक वर्ग का क्षेत्रफल क्या है?
- लेंस का कोणीय आवर्धन (आवर्धन क्षमता) क्या है?
- क्या (a) में आवर्धन क्षमता (b) में आवर्धन के बराबर है? स्पष्ट कीजिए।
वस्तु तथा आवर्धक लेंस के बीच कितनी दूरी होनी चाहिए ताकि आभासी प्रतिबिंब में प्रत्येक वर्ग 6.25 mm2 क्षेत्रफल का प्रतीत हो? क्या आप आवर्धक लेंस को नेत्र के अत्यधिक निकट रखकर इन वर्गों को सुस्पष्ट देख सकेंगे।
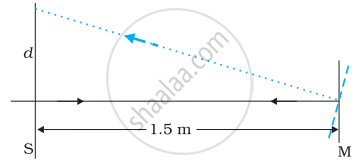
किसी गैल्वेनोमीटर की कुंडली से जुड़े समतल दर्पण पर लंबवत आपतित प्रकाश दर्पण से टकराकर अपना पथ पुनः अनुरेखित करता है। गैल्वेनोमीटर की कुंडली में प्रवाहित कोई धारा दर्पण में 3.5° का परिक्षेपण उत्पन्न करती है। दर्पण के सामने 1.5 m की दूरी पर रखे परदे पर प्रकाश के परावर्ती चिह्न में कितना विस्थापन होगा?
चित्र में कोई समोत्तल लेंस (अपवर्तनांक 1.50) किसी समतल दर्पण के फलक पर किसी द्रव की परत के संपर्क में दर्शाया गया है। कोई छोटी सुई जिसकी नोंक मुख्य अक्ष पर है, अक्ष के अनुदिश ऊपर-नीचे गति कराकर इस प्रकार समायोजित की जाती है कि सुई की नोंक का उल्टा प्रतिबिंब सुई की स्थिति पर ही बने। इस स्थिति में सुई की लेंस से दूरी 45.0 cm है। द्रव को हटाकर प्रयोग को दोहराया जाता है। नयी दूरी 30.0 cm मापी जाती है। द्रव का अपवर्तनांक क्या है?