Advertisements
Advertisements
Question
बिंदु A(2, 9), B(a, 5) और C(5, 5) एक त्रिभुज ABC के शीर्ष हैं, जिसका∠B समकोण है। a के मान ज्ञात कीजिए और फिर ΔABC का क्षेत्रफल ज्ञात कीजिए।
Solution
दिया गया है कि, बिंदु A(2, 9), B(a, 5) और C(5, 5) B पर समकोण ΔABC के शीर्ष हैं।
पाइथागोरस प्रमेय द्वारा,
AC2 = AB2 + BC2
अब, दूरी सूत्र द्वारा,
AB = `sqrt((a - 2)^2 + (5 - 9)^2)` ...(i) `[∵ "दो बिंदुओं के बीच की दूरी" (x_1, y_1) "और" (x_2, y_2) = sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)]`
= `sqrt(a^2 + 4 - 4a + 16)`
= `sqrt(a^2 - 4a + 20)`
BC = `sqrt((5 - a)^2 + (5 - 5)^2`
= `sqrt((5 - a)^2 + 0)`
= 5 – a
और AC = `sqrt((2 - 5)^2 + (9 - 5)^2`
= `sqrt((-3)^2 + (4)^2`
= `sqrt(9 + 16)`
= `sqrt(25)`
= 5
AB, BC और AC का मान समीकरण (i) में रखने पर, हमें प्राप्त होता है।
(5)2 = `(sqrt(a^2 - 4a + 20))^2 + (5 - a)^2`
⇒ 25 = a2 – 4a + 20 + 25 + a2 – 10a
⇒ 2a2 – 14a + 20 = 0
⇒ a2 – 7a + 10 = 0
⇒ a2 – 2a – 5a + 10 = 0 ...[गुणनखंडन विधि द्वारा]
⇒ a(a – 2) – 5(a – 2) = 0
⇒ (a – 2)(a – 5) = 0
∴ a = 2, 5
यहाँ, a ≠ 5, चूँकि a = 5 पर, BC की लंबाई = 0 है।
यह संभव नहीं है क्योंकि भुजाएँ AB, BC और CA एक समकोण त्रिभुज बनाती हैं।
तो, a = 2
अब, A, B और C का निर्देशांक क्रमशः (2, 9), (2, 5) और (5, 5) हो जाता है।
∵ ΔABC का क्षेत्रफल = `1/2[x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)]`
∴ Δ = `1/2[2(5 - 5) + 2(5 - 9) + 5(9 - 5)]`
= `1/2[2 xx 0 + 2(-4) + 5(4)]`
= `1/2(0 - 8 + 20)`
= `1/2 xx 12`
= 6
अतः, △ABC का अभीष्ट क्षेत्रफल 6 वर्ग इकाई है।
APPEARS IN
RELATED QUESTIONS
निम्नलिखित में से प्रत्येक में 'k' का मान ज्ञात कीजिए, ताकि तीनों बिंदु संरेखी हों:
(8, 1), (k, -4), (2, -5)
किसी त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है। उस त्रिभुज ABC के लिए इस परिणाम का सत्यापन कीजिए जिसके शीर्ष A(4, -6), B(3, -2) और C(5, 2) हैं।
x और y में एक संबंध ज्ञात कीजिए, यदि बिंदु (x, y), (1, 2) और (7, 0) संरेखी हैं।
कृष्णानगर के एक सेकेंडरी स्कूल के कक्षा X के विद्यार्थियों को उनके बागवानी क्रियाकलाप के लिए, एक आयताकार भूखंड दिया गया है। गुलमोहर की पौध (sapling) को परस्पर 1m की दूरी पर इस भूखंड की परिसीमा (boundary) पर लगाया जाता है। इस भूखंड के अंदर एक त्रिभुजाकार घास लगा हुआ लॉन (lawn) है, जैसाकि आकृति में दर्शाया गया है। विद्यार्थियों को भूखंड के शेष भाग में है फूलों के पौधे के बीज बोने हैं।
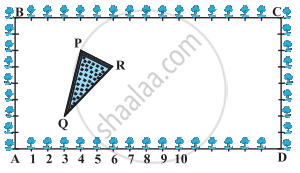
(i) A को मूलबिंदु मानते हए, त्रिभुज के शीषों के निर्देशांक ज्ञात कीजिए।
(ii) यदि मूलबिंदु C हो, तो ∆PQR के शीर्षों के निर्देशांक क्या होंगे?
साथ ही, उपरोक्त दोनों स्थितियों में, त्रिभुजों के क्षेत्रफल ज्ञात कीजिए। आप क्या देखते हैं?
एक त्रिभुज ABC के शीर्ष A(4, 6), B(1, 5) और C(7, 2) हैं। भुजाओं AB और AC को क्रमश: D और E पर प्रतिच्छेद करते हुए एक रेखा इस प्रकार खींची गई है कि `"AD"/"AB" = "AE"/"AC" = 1/4` है। ∆ADE का क्षेत्रफल परिकलित कीजिए और इसकी तुलना ∆ABC के क्षेत्रफल से कीजिए।
(प्रमेय 6.2 और प्रमेय 6.6 का स्मरण कीजिए।)
बिंदु (0, 5), (0, –9) और (3, 6) संरेख हैं।
बिंदु A(3, 1), B(12, –2) और C(0, 2) एक त्रिभुज के शीर्ष नहीं हो सकते।
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष (–8, 4), (–6, 6) और (–3, 9) हैं।
यदि बिंदु `D((-1)/2, 5/2) , E(7, 3)` और `F(7/2, 7/2)` एक त्रिभुज ABC की भुजाओं के मध्य-बिंदु हैं, तो ΔABC का क्षेत्रफल ज्ञात कीजिए।
आधार 4 cm और ऊँचाई 6 cm वाले त्रिभुज का क्षेत्रफल 24 cm2 है।
