Advertisements
Advertisements
Question
Calculate the change in angular momentum of the electron when it jumps from third orbit to first orbit in hydrogen atom.
(Take h = 6.33 × 10−34 Js)
Advertisements
Solution
According to Bohr's second postulate,
Angular momentum = `(nh)/(2 pi)`
For the first orbit, n1 = 1
∴ `L_1 = ((1)h)/(2 pi) = h/(2 pi)` ...(i)
For the third orbit, n3 = 3
∴ `L_3 = ((3)h)/(2 pi) = (3h)/(2 pi)` ...(ii)
When an electron jumps from 3rd orbit to 1st orbit, the change in angular momentum is
`L_3 - L_1 = (3 h)/(2 pi) - h/(2 pi)`
= `(2 h)/(2 pi)`
= `h / pi`
Putting h and π values, we get
Change in angular momentum = `(6.33 xx 10^-34)/3.142`
= 2.11 × 10−34 kg m2/s
The change in angular momentum of an electron when it jumps from the 3rd orbit to the 1st orbit in a hydrogen atom is 2.11 × 10−34 kg m2/s.
APPEARS IN
RELATED QUESTIONS
Obtain an expression for the torque acting on a rotating body with constant angular acceleration. Hence state the dimensions and SI unit of torque.
Obtain an expression for torque acting on a body rotating with uniform angular acceleration.
Define moment of inertia. State its SI unit and dimensions.
A 500 kg car takes a round turn of the radius of 50m with a velocity of 36 km/hr. The centripetal force is ______.
A flywheel of mass 8 kg and radius 10 cm rotating with a uniform angular speed of 5 rad/sec about its axis of rotation, is subjected to an accelerating torque of 0.01 Nm for 10 seconds. Calculate the change in its angular momentum and change in its kinetic energy.
A stone of mass 1 kg is rotated in a horizontal circle of radius 0.5 m. If it makes `100/pi` rps, then its angular momentum is ______
A charged particle (charge = q: mass = m) is rotating in a circle of radius 'R' with uniform speed 'v'. The ratio of its magnetic moment (M) to the angular momentum (L) is ______
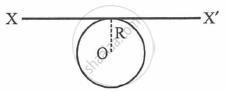
A thin metal wire of length 'L' and uniform linear mass density 'ρ' is bent into a circular coil with 'O' as centre. The moment of inertia of a coil about the axis XX' is ______.
The angular momentum of electron in hydrogen atom is proportional to ____________.
If the kinetic energy of rotation of a body is doubled, then its angular momentum ____________.
Two bodies with moments of inertia I1 and I2 (I1 > I2) have equal angular momenta. lf E1 and E2 are their rotational kinetic energies respectively, then ____________.
The ratio of the dimensions of Planck's constant to that of moment of inertia is the dimensions of ______.
A particle of mass m is rotating in a plane in a circular path of radius r. Its angular momentum is L. The centripetal force acting on the particle is ______.
If the angular momentum of an electron is `vec"J"` then the magnitude of the magnetic moment will be ____________.
Let I1 and I2 be the moments of inertia of two bodies of identical geometrical shape. If the first body is made of aluminium and the second of iron, then ____________.
mass is whirled in a circular path with constant angular velocity and its linear velocity is v. If the string is now halved keeping the angular momentum same, the linear velocity is ______.
An electron has a mass of 9.1 x 10-31 kg. It revolves round the nucleus in a circular orbit of radius 0.529 x 10-10 metre at a speed of 2.2 x 106 m/s. The magnitude of its linear momentum in this motion is ____________.
A particle is revolving in anticlockwise sense along the circumference of a circle of radius 'r' with linear velocity 'v', then the angle between 'v' and angular velocity 'ω' will be ______.
If E, M and P are the kinetic energy, mass and linear momentum of a particle respectively, which of the following relations represents the angular momentum L of the particle when the particle rotates in a circle of radius R?
An electron in an atom is revolving round the nucleus in a circular orbit of radius 5.3 × 10-11 m with a speed of 3 × 106 m/s. Find the angular momentum of electron.
A body is rotating about its own axis. Its rotational kinetic energy is x and its angular momentum is y, hence its moment of inertia about the axis is ______.
A particle of mass m = 5 unit is moving with a uniform speed v = 3`sqrt2` unit in the XY-plane along the line y = x + 4. The magnitude of the angular momentum about origin is ______.
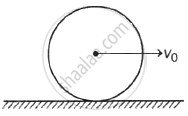
A sphere rolls without slipping on a rough horizontal surface with centre of mass speed v0. If mass of the sphere is M and its radius is R, then what is the angular momentum of the sphere about the point of contact?
The angular momentum of the electron in the second orbit of hydrogen atom is L. The angular momentum in the third orbit is ______.
Define angular momentum.
