Advertisements
Advertisements
Question
Choose the correct alternative:
The point at which the maximum value of Z = 4x + 6y subject to the constraints 3x + 2y ≤ 12, x + y ≥ 4, x ≥ 0, y ≥ 0 is obtained at the point
Options
(0, 6)
(6, 0)
(0, 4)
(4, 0)
Solution
(0, 6)
APPEARS IN
RELATED QUESTIONS
A small manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry, then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for the production of each unit of A and B, and the number of man-hours the firm has available per week are as follows:
| Gadget | Foundry | Machine-shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Firm's capacity per week | 1000 | 600 |
The profit on the sale of A is Rs 30 per unit as compared with Rs 20 per unit of B. The problem is to determine the weekly production of gadgets A and B, so that the total profit is maximized. Formulate this problem as a LPP.
A firm manufactures two products, each of which must be processed through two departments, 1 and 2. The hourly requirements per unit for each product in each department, the weekly capacities in each department, selling price per unit, labour cost per unit, and raw material cost per unit are summarized as follows:
| Product A | Product B | Weekly capacity | |
| Department 1 | 3 | 2 | 130 |
| Department 2 | 4 | 6 | 260 |
| Selling price per unit | ₹ 25 | ₹ 30 | |
| Labour cost per unit | ₹ 16 | ₹ 20 | |
| Raw material cost per unit | ₹ 4 | ₹ 4 |
The problem is to determine the number of units to produce each product so as to maximize total contribution to profit. Formulate this as a LPP.
Solve the following LPP by graphical method:
Maximize z = 11x + 8y, subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0
Solve the following L.P.P. by graphical method :
Maximize: Z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find maximum value of Z.
Choose the correct alternative :
The maximum value of z = 5x + 3y. subject to the constraints
The region represented by the inequality y ≤ 0 lies in _______ quadrants.
State whether the following is True or False :
The region represented by the inqualities x ≤ 0, y ≤ 0 lies in first quadrant.
Solve the following problem :
A factory produced two types of chemicals A and B The following table gives the units of ingredients P & Q (per kg) of Chemicals A and B as well as minimum requirements of P and Q and also cost per kg. of chemicals A and B.
| Ingredients per kg. /Chemical Units | A (x) |
B (y) |
Minimum requirements in |
| P | 1 | 2 | 80 |
| Q | 3 | 1 | 75 |
| Cost (in ₹) | 4 | 6 |
Find the number of units of chemicals A and B should be produced so as to minimize the cost.
Solve the following problem :
A Company produces mixers and processors Profit on selling one mixer and one food processor is ₹ 2000 and ₹ 3000 respectively. Both the products are processed through three machines A, B, C The time required in hours by each product and total time available in hours per week on each machine are as follows:
| Machine/Product | Mixer per unit | Food processor per unit | Available time |
| A | 3 | 3 | 36 |
| B | 5 | 2 | 50 |
| C | 2 | 6 | 60 |
How many mixers and food processors should be produced to maximize the profit?
State whether the following statement is True or False:
The maximum value of Z = 5x + 3y subjected to constraints 3x + y ≤ 12, 2x + 3y ≤ 18, 0 ≤ x, y is 20
State whether the following statement is True or False:
If LPP has two optimal solutions, then the LPP has infinitely many solutions
A set of values of variables satisfying all the constraints of LPP is known as ______
Smita is a diet conscious house wife, wishes to ensure certain minimum intake of vitamins A, B and C for the family. The minimum daily needs of vitamins A, B, and C for the family are 30, 20, and 16 units respectively. For the supply of the minimum vitamin requirements Smita relies on 2 types of foods F1 and F2. F1 provides 7, 5 and 2 units of A, B, C vitamins per 10 grams and F2 provides 2, 4 and 8 units of A, B and C vitamins per 10 grams. F1 costs ₹ 3 and F2 costs ₹ 2 per 10 grams. How many grams of each F1 and F2 should buy every day to keep her food bill minimum
A wholesale dealer deals in two kinds of mixtures A and B of nuts. Each kg of mixture A contains 60 grams of almonds, 30 grams of cashew and 30 grams of hazel nuts. Each kg of mixture B contains 30 grams of almonds, 60 grams of cashew and 180 grams of hazel nuts. A dealer is contemplating to use mixtures A and B to make a bag which will contain at least 240 grams of almonds, 300 grams of cashew and 540 grams of hazel nuts. Mixture A costs ₹ 8 and B costs ₹ 12 per kg. How many kgs of each mixture should he use to minimize the cost of the kgs
Maximize Z = 5x + 10y subject to constraints
x + 2y ≤ 10, 3x + y ≤ 12, x ≥ 0, y ≥ 0
Maximize Z = 400x + 500y subject to constraints
x + 2y ≤ 80, 2x + y ≤ 90, x ≥ 0, y ≥ 0
Minimize Z = 24x + 40y subject to constraints
6x + 8y ≥ 96, 7x + 12y ≥ 168, x ≥ 0, y ≥ 0
Solve the LPP graphically:
Minimize Z = 4x + 5y
Subject to the constraints 5x + y ≥ 10, x + y ≥ 6, x + 4y ≥ 12, x, y ≥ 0
Solution: Convert the constraints into equations and find the intercept made by each one of it.
| Inequations | Equations | X intercept | Y intercept | Region |
| 5x + y ≥ 10 | 5x + y = 10 | ( ___, 0) | (0, 10) | Away from origin |
| x + y ≥ 6 | x + y = 6 | (6, 0) | (0, ___ ) | Away from origin |
| x + 4y ≥ 12 | x + 4y = 12 | (12, 0) | (0, 3) | Away from origin |
| x, y ≥ 0 | x = 0, y = 0 | x = 0 | y = 0 | 1st quadrant |
∵ Origin has not satisfied the inequations.
∴ Solution of the inequations is away from origin.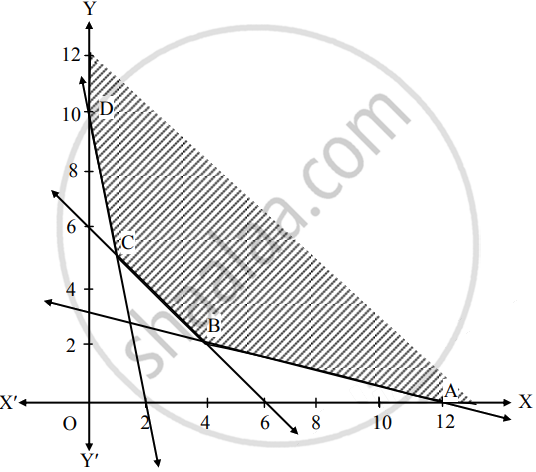
The feasible region is unbounded area which is satisfied by all constraints.
In the figure, ABCD represents
The set of the feasible solution where
A(12, 0), B( ___, ___ ), C ( ___, ___ ) and D(0, 10).
The coordinates of B are obtained by solving equations
x + 4y = 12 and x + y = 6
The coordinates of C are obtained by solving equations
5x + y = 10 and x + y = 6
Hence the optimum solution lies at the extreme points.
The optimal solution is in the following table:
| Point | Coordinates | Z = 4x + 5y | Values | Remark |
| A | (12, 0) | 4(12) + 5(0) | 48 | |
| B | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | ______ |
| C | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | |
| D | (0, 10) | 4(0) + 5(10) | 50 |
∴ Z is minimum at ___ ( ___, ___ ) with the value ___
Maximised value of z in z = 3x + 4y, subject to constraints : x + y ≤ 4, x ≥ 0. y ≥ 0
