Advertisements
Advertisements
Question
\[\frac{dy}{dx} = x^2 e^x\]
Solution
We have,
\[\frac{dy}{dx} = x^2 e^x \]
\[ \Rightarrow dy = x^2 e^x dx\]
Integrating both sides, we get
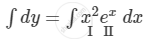
\[ \Rightarrow \int dy = x^2 \int e^x dx - \int\left( \frac{d}{dx}\left( x^2 \right)\int e^x dx \right)dx\]
\[ \Rightarrow y = x^2 e^x - 2\int x e^x dx\]
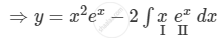
\[ \Rightarrow y = x^2 e^x - 2x\int e^x dx + 2\int\left( \frac{d}{dx}\left( x \right)\int e^x dx \right)dx\]
\[ \Rightarrow y = x^2 e^x - 2x e^x + 2 e^x + C\]
\[ \Rightarrow y = \left( x^2 - 2x + 2 \right) e^x + C\]
APPEARS IN
RELATED QUESTIONS
Write the integrating factor of the following differential equation:
(1+y2) dx−(tan−1 y−x) dy=0
Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
y = a e3x + b e– 2x
Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
y = e2x (a + bx)
Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
y = ex (a cos x + b sin x)
The general solution of a differential equation of the type `dx/dy + P_1 x = Q_1` is ______.
The general solution of the differential equation ex dy + (y ex + 2x) dx = 0 is ______.
Find the differential equation of all the circles which pass through the origin and whose centres lie on x-axis.
Form the differential equation having \[y = \left( \sin^{- 1} x \right)^2 + A \cos^{- 1} x + B\], where A and B are arbitrary constants, as its general solution.
The equation of the curve satisfying the differential equation y (x + y3) dx = x (y3 − x) dy and passing through the point (1, 1) is
Show that y = C x + 2C2 is a solution of the differential equation \[2 \left( \frac{dy}{dx} \right)^2 + x\frac{dy}{dx} - y = 0.\]
Show that y2 − x2 − xy = a is a solution of the differential equation \[\left( x - 2y \right)\frac{dy}{dx} + 2x + y = 0.\]
Verify that y = A cos x + sin x satisfies the differential equation \[\cos x\frac{dy}{dx} + \left( \sin x \right)y=1.\]
Find the differential equation corresponding to y = ae2x + be−3x + cex where a, b, c are arbitrary constants.
Show that the differential equation of all parabolas which have their axes parallel to y-axis is \[\frac{d^3 y}{d x^3} = 0.\]
\[\frac{dy}{dx} = \frac{1}{x^2 + 4x + 5}\]
\[\frac{dy}{dx} = y^2 + 2y + 2\]
\[\frac{dy}{dx} + 4x = e^x\]
\[\frac{dy}{dx} - x \sin^2 x = \frac{1}{x \log x}\]
\[(\tan^2 x + 2\tan x + 5)\frac{dy}{dx} = 2(1+\tan x)\sec^2x\]
tan y dx + tan x dy = 0
cos y log (sec x + tan x) dx = cos x log (sec y + tan y) dy
Find the general solution of the differential equation `"dy"/"dx" = y/x`.
A solution of the differential equation `("dy"/"dx")^2 - x "dy"/"dx" + y` = 0 is ______.
The general solution of the differential equation `(dy)/(dx) + x/y` = 0 is
General solution of tan 5θ = cot 2θ is
The number of arbitrary constant in the general solution of a differential equation of fourth order are
The general solution of the differential equation `(dy)/(dx) = e^(x + y)` is
The general solution of the differential equation `(ydx - xdy)/y` = 0
The general solution of the differential equation `x^xdy + (ye^x + 2x) dx` = 0
Find the general solution of differential equation `(dy)/(dx) = (1 - cosx)/(1 + cosx)`
What is the general solution of differential equation `(dy)/(dx) = sqrt(4 - y^2) (-2 < y < 2)`
The general solution of the differential equation ydx – xdy = 0; (Given x, y > 0), is of the form
(Where 'c' is an arbitrary positive constant of integration)
