Advertisements
Advertisements
Question
The photoelectric threshold wavelength of a metal is 230 nm. Determine the maximum kinetic energy in joule and in eV of the ejects electron for the metal surface when it is exposed to a radiation of wavelength 180 nm.
[Planck’s constant : h = 6.63 * 10-34 Js, Velocity of light : C = 3 * 108 m/s.]
Solution
λ0 = 230 nm = 230 × 10−9m,
λ = 180 nm = 180 × 10−9m,
h = 6.63 × 10−34 J s, c = 3 × 108
m/s, K.E. (in joule and eV) = ?
Now,

∴ The maximum kinetic energy of the ejected electron is 2.402 × 10−19 J.

∴ The maximum kinetic energy of the ejected electron is 1.5 eV.
APPEARS IN
RELATED QUESTIONS
The energy of photon of wavelength X is_____ .
[h = Planck’s constant, c = speed of light in vacuum]
The momentum of a photon of de Broglie wavelength 5000Å is _______.
[Planck’s constant = 6.63 x10-34 J.s.]
Find the wave number of a photon having energy of 2.072 eV
Given : Charge on electron = 1.6 x 10-19 C,
Velocity of light in air = 3 x 108 m/s,
Planck’s constant = 6.63 x 10-34 J-s.
State two important properties of photon which are used to write Einstein’s photoelectric equation.
Define (i) stopping potential and (ii) threshold frequency, using Einstein’s equation and drawing necessary plot between relevant quantities.
Write its S.I. unit of (intensity of radiation)
Radiation of frequency 1015 Hz is incident on two photosensitive surface P and Q. There is no photoemission from surface P. Photoemission occurs from surface Q but photoelectrons have zero kinetic energy. Explain these observations and find the value of work function for surface Q.
Write the basic features of photon picture of electromagnetic radiation on which Einstein’s photoelectric equation is based.
Write Einstein’s photoelectric equation.
According to Einstein’s model minimum energy needed for the electron to escape from a metal surface having work function ϕ0, the electron is emitted with maximum kinetic energy, Kmax = ______.
According to the Einstein’s model, stopping potential Vo for a metal having work function ϕ0 is given by ______.
Which of the following graphs correctly represents the variation of maximum kinetic energy (Ek) of photoelectrons with the frequency (𝜈) of the incident radiation?
A police van moving on a highway with a speed of 30 km/h fires a bullet at a thief's car speeding away in the same direction with a speed of 192 km/h. If the muzzle speed of the bullet is 150 m is, with what speed does the bullet hit the thief's car?
A 200 W sodium street lamp emits yellow light of wavelength 0.6 µm. Assuming it to be 25% efficient in converting electrical energy to light, the number of photons of yellow light it emits per second is:
Dimensions of ‘resistance’ are same as (where h is Planck's constant and e is charge):
Threshold frequency for photoelectric effect on sodium corresponds to a wave length 5000. Its work function is ______.
Einstein work on the photoelectric effect provided support for the eqn:-
If the frequency of light in a photoelectric experiment is double the stopping potential will
If the energy of photon corresponding to a wavelength of 6000 A° is 3.32 × 10-19 J, the photon energy for a wavelength of 4000 A° will be
The slope of frequency of incident light and stopping potential for a given surface will be
Which of the following is/are true for cathode ray
The moment of a photon is given by
- Calculate the frequency of a photon of energy 6.5 × 10−19 J.
- Can this photon cause the emission of an electron from the surface of Cs of work function 2.14 eV? If yes, what will be the maximum kinetic energy of the photoelectron?
Ultraviolet light is incident on metals P, Q and R, having work functions 8 eV, 2 eV and 4 eV respectively,
- Which metal has lowest threshold frequency for photoelectric effect?
- For which metal is the value of Emax minimum?
(Note: Emax is maximum kinetic energy of the emitted photoelectrons.)
How does stopping potential in photoelectric emission vary if the intensity of the incident radiation increases?
The graphs below show the variation of the stopping potential VS with the frequency (ν) of the incident radiations for two different photosensitive materials M1 and M2.
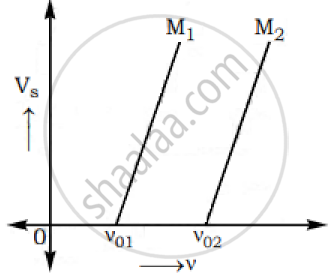
Express work function for M1 and M2 in terms of Planck’s constant(h) and Threshold frequency and charge of the electron (e).
If the values of stopping potential for M1 and M2 are V1 and V2 respectively then show that the slope of the lines equals to `(V_1-V_2)/(V_(01)-V_(02))` for a frequency,
ν > ν02 and also ν > ν01
