Advertisements
Advertisements
Question
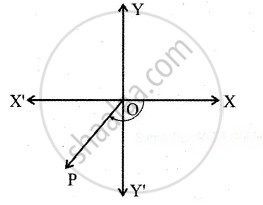
Determine the quadrant in which the following degree lie.
-140°
Solution
-140° = -90° + (-50°)
The angle is negative it moves in the anti-clockwise direction.
-140° lies in the III quadrants.
APPEARS IN
RELATED QUESTIONS
Convert the following degree measure into radian measure.
150°
Convert the following degree measure into radian measure.
60°
Find the degree measure corresponding to the following radian measure.
`pi/8`
Determine the quadrant in which the following degree lie.
1195°
Prove that:
2 sin2 `pi/6` + cosec2 `(7pi)/6` cos2 `pi/3 = 3/2`
Prove that:
`sin theta * cos theta {sin(pi/2 - theta) * "cosec" theta + cos (pi/2 - theta) * sec theta}` = 1
Prove that: cos 510° cos 330° + sin 390° cos 120° = -1.
Prove that:
`(sin(180^circ + "A")cos(90^circ - "A")tan(270^circ - "A"))/(sec(540^circ - "A") cos(360^circ + "A") "cosec"(270^circ + "A"))` = - sin A cos2 A.
The value of `1/("cosec" (-45^circ))` is:
`((cos x)/(cosec x)) - sqrt(1 - sin^2x) sqrt(1 - cos^2 x)` is:
