Advertisements
Advertisements
Question
Explain whether a gas approaches ideal behavior or deviates from ideal behaviour if it is compressed to a smaller volume at a constant temperature.
Solution
When the gas is compressed to a smaller volume, the compressibility factor (Z) decreases. Hence, the gas deviates from ideal behavior.
APPEARS IN
RELATED QUESTIONS
Calculate the volume occupied by 8.8 g of CO2 at 31.1°C and 1 bar pressure. R = 0.083 bar L K–1 mol–1.
Compressibility factor for CO2 at 400 K and 71.0 bar is 0.8697. The molar volume of CO2 under these conditions is
Can a Van der Waals gas with a = 0 be liquefied? explain.
Explain whether a gas approaches ideal behavior or deviates from ideal behaviour if the temperature is raised while keeping the volume constant.
Explain whether a gas approaches ideal behavior or deviates from ideal behaviour if more gas is introduced into the same volume and at the same temperature.
Which of the following gases would you expect to deviate from ideal behavior under conditions of low-temperature F2, Cl2, or Br2? Explain.
A plot of volume (V) versus temperature (T) for a gas at constant pressure is a straight line passing through the origin. The plots at different values of pressure are shown in Figure. Which of the following order of pressure is correct for this gas?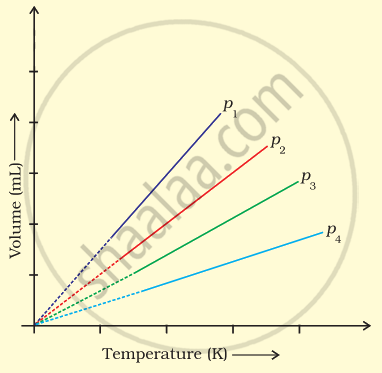
Compressibility factor, Z, of a gas is given as Z = `(pV)/(nRT)`. What is the value of Z for an ideal gas?
Pressure versus volume graph for a real gas and an ideal gas are shown in figure. Answer the following questions on the basis of this graph.
(i) Interpret the behaviour of real gas with respect to ideal gas at low pressure.
(ii) Interpret the behaviour of real gas with respect to ideal gas at high pressure.
(iii) Mark the pressure and volume by drawing a line at the point where real gas behaves as an ideal gas.
Assertion (A): At constant temperature, pV vs V plot for real gases is not a straight line.
Reason (R): At high pressure all gases have \[\ce{Z}\] > 1 but at intermediate pressure most gases have \[\ce{Z}\] < 1.
