Advertisements
Advertisements
Question
Find the electric force between two protons separated by a distance of 1 fermi (1 fermi = 10−15 m). The protons in a nucleus remain at a separation of this order.
Solution
We know:
Charge on a proton, q = 1.6 × 10−19 C
Given, separation between the charges, r = 10−15 m
By Coulomb's Law, electrostatic force,
\[F = \frac{1}{4\pi \epsilon_0}\frac{q_1 q_2}{r^2}\]
\[\Rightarrow F = 9 \times {10}^9 \times \frac{\left( 1 . 6 \times {10}^{- 19} \right)^2}{\left( {10}^{- 15} \right)^2}\]
\[ \Rightarrow F = 230 N\]
APPEARS IN
RELATED QUESTIONS
Suppose that the particle is an electron projected with velocity vx = 2.0 × 106 m s−1. If E between the plates separated by 0.5 cm is 9.1 × 102 N/C, where will the electron strike the upper plate? (|e| = 1.6 × 10−19 C, me = 9.1 × 10−31 kg)
Three-point charges q, – 4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q

(b) Find out the amount of the work done to separate the charges at infinite distance.
Write any two important points of similarities and differences each between Coulomb's law for the electrostatic field and Biot-Savart's law of the magnetic field ?
Two charges 2.0 × 10−6 C and 1.0 × 10−6 C are placed at a separation of 10 cm. Where should a third charge be placed, such that it experiences no net force due to these charges?
Suppose the second charge in the previous problem is −1.0 × 10−6 C. Locate the position where a third charge will not experience a net force.
Four equal charges of 2.0 × 10−6 C each are fixed at the four corners of a square of side 5 cm. Find the Coulomb's force experienced by one of the charges due to the other three.
A hydrogen atom contains one proton and one electron. It may be assumed that the electron revolves in a circle of radius 0.53 angstrom (1 angstrom = 10−10 m and is abbreviated as Å ) with the proton at the centre. The hydrogen atom is said to be in the ground state in this case. Find the magnitude of the electric force between the proton and the electron of a hydrogen atom in its ground state.
Two identical pith balls are charged by rubbing one against the other. They are suspended from a horizontal rod through two strings of length 20 cm each, the separation between the suspension points being 5 cm. In equilibrium, the separation between the balls is 3 cm. Find the mass of each ball and the tension in the strings. The charge on each ball has a magnitude 2.0 × 10−8 C.
Two identical pith balls, each carrying a charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
Two particles A and B, each carrying a charge Q, are held fixed with a separation dbetween them. A particle C of mass m and charge q is kept at the middle point of the line AB. Assuming x<<d, show that this force is proportional to x.
How much work has to be done in assembling three charged particles at the vertices of an equilateral triangle, as shown in the figure?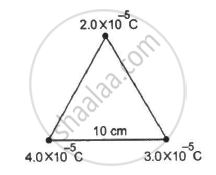
Write down Coulomb’s law in vector form and mention what each term represents.
A force F acts between sodium and chlorine ions of salt (sodium chloride) when put 1 cm apart in air. The permittivity of air and dielectric constant of water are `epsilon_0` and K respectively. When a piece of salt is put in water, electrical force acting between sodium and chlorine ions 1 cm apart is ____________.
Two positive charges ______.
A spring of spring constant 5 × 103 N/m is stretched initially by 5 cm from the unstretched position. Then the work required to stretch it further by another 5 cm is:
Two charge – 10c and + 10 c are placed 10 cm apart. Potential at centre of the line joining the two charge is:-
Identify the wrong statement in the following.
Coulomb's law correctly describes the electric force that ______
There is another useful system of units, besides the SI/mks A system, called the cgs (centimeter-gram-second) system. In this system Coloumb’s law is given by
F = `(Qq)/r^2 hatr`
where the distance r is measured in cm (= 10–2 m), F in dynes (= 10–5 N) and the charges in electrostatic units (es units), where 1 es unit of charge = `1/([3]) xx 10^-9 C`
The number [3] actually arises from the speed of light in vaccum which is now taken to be exactly given by c = 2.99792458 × 108 m/s. An approximate value of c then is c = [3] × 108 m/s.
(i) Show that the coloumb law in cgs units yields
1 esu of charge = 1 (dyne)1/2 cm.
Obtain the dimensions of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L.
(ii) Write 1 esu of charge = x C, where x is a dimensionless number. Show that this gives
`1/(4pi ∈_0) = 10^-9/x^2 (N*m^2)/C^2`
With `x = 1/([3]) xx 10^-9`, we have `1/(4pi ∈_0) = [3]^2 xx 10^9 (Nm^2)/C^2`
or, `1/(4pi ∈_0) = (2.99792458)^2 xx 10^9 (Nm^2)/C^2` (exactly).
Which of the following statements about nuclear forces is not true?
