Advertisements
Advertisements
Question
Four equal charges of 2.0 × 10−6 C each are fixed at the four corners of a square of side 5 cm. Find the Coulomb's force experienced by one of the charges due to the other three.
Solution
Given,
Magnitude of the charges,
\[q = 2 \times {10}^{- 6} C\] Side of the square,
\[a = 5 \text{ cm = 0 . 05 m }\]
By Coulomb's Law, force,
\[F = \frac{1}{4\pi \epsilon_0}\frac{q_1 q_2}{r^2}\]
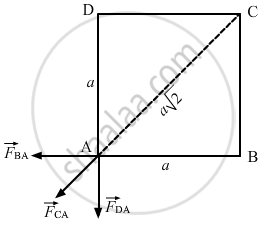
So, force on the charge at A due to the charge at B,
\[\vec{F}_{BA} = \frac{9 \times {10}^9 \times \left( 2 \times {10}^{- 6} \right)^2}{\left( 0 . 05 \right)^2} \]
\[ = \frac{9 \times {10}^9 \times 4 \times {10}^{- 12}}{25 \times {10}^{- 4}}\]
\[ = 14 . 4 N\]
Force on the charge at A due to the charge at C,
\[\vec{F}_{CA} = \frac{9 \times {10}^9 \times \left( 2 \times {10}^{- 6} \right)^2}{\left( \sqrt{2} \times 0 . 05 \right)^2}\]
\[ = \frac{9 \times {10}^9 \times 4 \times {10}^{- 12}}{25 \times 2 \times {10}^{- 4}}\]
\[ = 7 . 2 N\]
Force on the charge at A due to the charge at D,
\[\vec{F}_{DA} = \vec{F}_{BA}\]
The resultant force at A, F'= \[\vec{F}_{BA} + \vec{F}_{CA} + \vec{F}_{DA}\]
The resultant force of \[\vec{F}_{DA} \text{ and } \vec{F}_{BA}\] will be \[\sqrt{2} F_{BA}\] in the direction of \[\vec{F}_{CA}\] . Hence, the resultant force,
\[F' = 14 . 4\sqrt{2} + 7 . 2\]
\[ = 27 . 56 N\]
APPEARS IN
RELATED QUESTIONS
Check that the ratio ke2/G memp is dimensionless. Look up a Table of Physical Constants and determine the value of this ratio. What does the ratio signify?
A particle of mass m and charge (−q) enters the region between the two charged plates initially moving along x-axis with speed vx (like particle 1 in the fig.). The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL2/(2m`"v"_"x"^2`).

Two charged particles with charge 2.0 × 10−8 C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
Two identical pith balls are charged by rubbing one against the other. They are suspended from a horizontal rod through two strings of length 20 cm each, the separation between the suspension points being 5 cm. In equilibrium, the separation between the balls is 3 cm. Find the mass of each ball and the tension in the strings. The charge on each ball has a magnitude 2.0 × 10−8 C.
Two identically-charged particles are fastened to the two ends of a spring of spring constant 100 N m−1 and natural length 10 cm. The system rests on a smooth horizontal table. If the charge on each particle is 2.0 × 10−8 C, find the extension in the length of the spring. Assume that the extension is small as compared to the natural length. Justify this assumption after you solve the problem.
Two particles A and B, each carrying a charge Q, are held fixed with a separation dbetween them. A particle C of mass m and charge q is kept at the middle point of the line AB. Assuming x<<d, show that this force is proportional to x.
Repeat the previous problem if the particle C is displaced through a distance x along the line AB.
Two particles A and B possessing charges of +2.00 × 10−6 C and of −4.00 × 10−6 C, respectively, are held fixed at a separation of 20.0 cm. Locate the points (s) on the line AB, where (a) the electric field is zero (b) the electric potential is zero.
A point charge produces an electric field of magnitude 5.0 NC−1 at a distance of 40 cm from it. What is the magnitude of the charge?
Two identical particles, each with a charge of 2.0 × 10−4 C and mass of 10 g, are kept at a separation of 10 cm and then released. What would be the speed of the particles when the separation becomes large?
Two-point charges of + 0.2 µµC and -0.2 µµC are separated by 1 o8 m. What is the value of the electric field at an axial point at a distance of 0.1 m from their mid-point?
Two point charges +3 µC and +8 µC repel each other with a force of 40 N. If a charge of -5 µC is added to each of them, then force between them will become ______.
SI unit of permittivity of free space is ______.
Two charges of equal magnitudes kept at a distance r exert a force F on each other. If the charges are halved and distance between them is doubled, then the new force acting on each charge is ______.
A spring of spring constant 5 × 103 N/m is stretched initially by 5 cm from the unstretched position. Then the work required to stretch it further by another 5 cm is:
The capacity of an isolate conducting sphere of radius R is proportional to
The S.I unit of electric permittivity is
Electric charge of any system is ______.
Two point charges Q each are placed at a distance d apart. A third point charge q is placed at a distance x from the mid-point on the perpendicular bisector. The value of x at which charge q will experience the maximum Coulomb's force is ______.
Two point charges +2 C and +6 C repel each other with a force of 12 N. If a charge of -4 C is given to each of these charges, then the force now is ______.
