Advertisements
Advertisements
Question
Find the area of the triangle formed by the line joining the vertex of the parabola x2 = 12y to the end points of latus rectum.
Solution
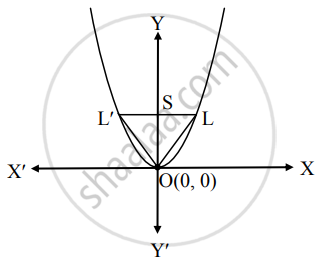
Given equation of the parabola is x2 = 12y.
Comparing this equation with x2 = 4by, we get
4b = 12
∴ b = 3
∴ The co-ordinates of focus are S(0, b), i.e., S(0, 3)
End points of the latus rectum are L(2b, b) and L′(– 2b, b),
i.e., L(6, 3) and L′(– 6, 3)
Also l(LL′) = length of latus rectum
= 4b
= 12
l(OS) = b = 3
Area of the ΔOLL′ = `1/2 xx l("LL"^′) xx l("OS")`
= `1/2 xx 12 xx 3`
∴ Area of the ΔOLL’ = 18 sq. units.
APPEARS IN
RELATED QUESTIONS
Find co-ordinate of focus, equation of directrix, length of latus rectum and the co-ordinate of end points of latus rectum of the parabola:
3x2 = 8y
Find the equation of the parabola with vertex at the origin, axis along X-axis and passing through the point (2, 3)
For the parabola 3y2 = 16x, find the parameter of the point (27, –12).
Find the focal distance of a point on the parabola y2 = 16x whose ordinate is 2 times the abscissa
Find coordinates of the point on the parabola. Also, find focal distance.
y2 = 12x whose parameter is `1/3`
Find length of latus rectum of the parabola y2 = 4ax passing through the point (2, –6)
If a parabolic reflector is 20 cm in diameter and 5 cm deep, find its focus.
Find coordinate of focus, vertex and equation of directrix and the axis of the parabola y = x2 – 2x + 3
Find the equation of tangent to the parabola y2 = 12x from the point (2, 5)
Find the equation of tangent to the parabola y2 = 36x from the point (2, 9)
Two tangents to the parabola y2 = 8x meet the tangents at the vertex in the point P and Q. If PQ = 4, prove that the equation of the locus of the point of intersection of two tangent is y2 = 8(x + 2).
Find the equation of common tangent to the parabola y2 = 4x and x2 = 32y
A circle whose centre is (4, –1) passes through the focus of the parabola x2 + 16y = 0.
Show that the circle touches the directrix of the parabola.
Select the correct option from the given alternatives:
The line y = mx + 1 is a tangent to the parabola y2 = 4x, if m is _______
Select the correct option from the given alternatives:
The endpoints of latus rectum of the parabola y2 = 24x are _______
Select the correct option from the given alternatives:
Equation of the parabola with vertex at the origin and directrix x + 8 = 0 is __________
Answer the following:
Find the Cartesian coordinates of the point on the parabola y2 = 12x whose parameter is 2
Answer the following:
Find the Cartesian coordinates of the point on the parabola y2 = 12x whose parameter is −3
Answer the following:
Find the equation of the tangent to the parabola y2 = 9x at the point (4, −6) on it
Answer the following:
Find the equation of the tangent to the parabola y2 = 8x at t = 1 on it
Answer the following:
Find the equation of the tangent to the parabola y2 = 8x which is parallel to the line 2x + 2y + 5 = 0. Find its point of contact
Answer the following:
The slopes of the tangents drawn from P to the parabola y2 = 4ax are m1 and m2, show that m1 − m2 = k, where k is a constant.
Answer the following:
The slopes of the tangents drawn from P to the parabola y2 = 4ax are m1 and m2, show that `("m"_1 /"m"_2)` = k, where k is a constant.
Answer the following:
Find the
(i) lengths of the principal axes
(ii) co-ordinates of the foci
(iii) equations of directrices
(iv) length of the latus rectum
(v) Distance between foci
(vi) distance between directrices of the curve
16x2 + 25y2 = 400
Answer the following:
Find the
(i) lengths of the principal axes
(ii) co-ordinates of the foci
(iii) equations of directrices
(iv) length of the latus rectum
(v) Distance between foci
(vi) distance between directrices of the curve
`x^2/144 - y^2/25` = 1
The area of the triangle formed by the lines joining vertex of the parabola x2 = 12y to the extremities of its latus rectum is ______.
Let P: y2 = 4ax, a > 0 be a parabola with focus S. Let the tangents to the parabola P make an angle of `π/4` with the line y = 3x + 5 touch the parabola P at A and B. Then the value of a for which A, B and S are collinear is ______.
If the normal at the point (1, 2) on the parabola y2 = 4x meets the parabola again at the point (t2, 2t), then t is equal to ______.
The centre of the circle passing through the point (0, 1) and touching the parabola y = x2 at the point (2, 4) is ______.
Which of the following are not parametric coordinates of any point on the parabola y2 = 4ax?
Let a variable point A be lying on the directrix of parabola y2 = 4ax (a > 0). Tangents AB and AC are drawn to the curve where B and C are points of contact of tangents. The locus of centroid of ΔABC is a conic whose length of latus rectum is λ, then `λ/"a"` is equal to ______.
A circle of radius 2 unit passes through the vertex and the focus of the parabola y2 = 2x and touches the parabola y = `(x - 1/4)^2 + α`, where α > 0. Then (4α – 8)2 is equal to ______.
Two parabolas with a common vertex and with axes along x-axis and y-axis, respectively, intersect each other in the first quadrant. if the length of the latus rectum of each parabola is 3, then the equation of the common tangent to the two parabolas is ______.
